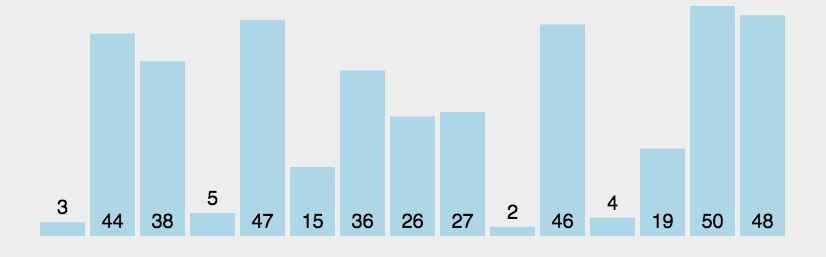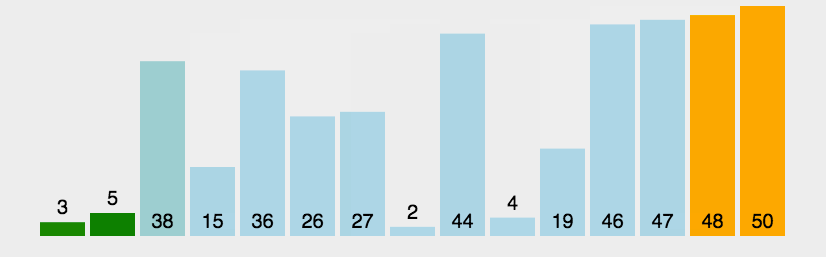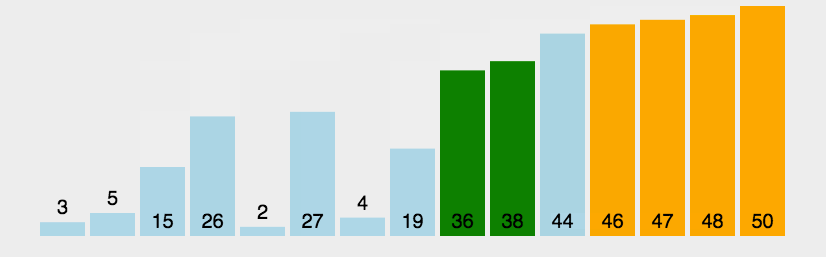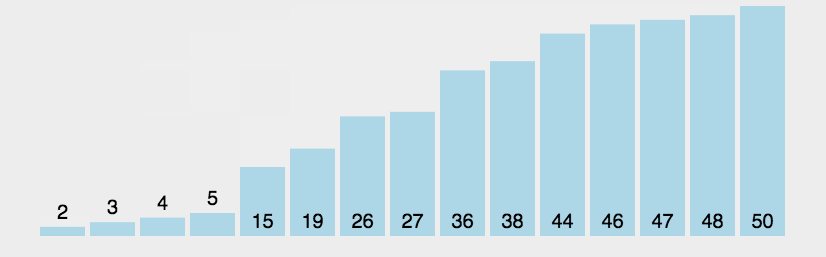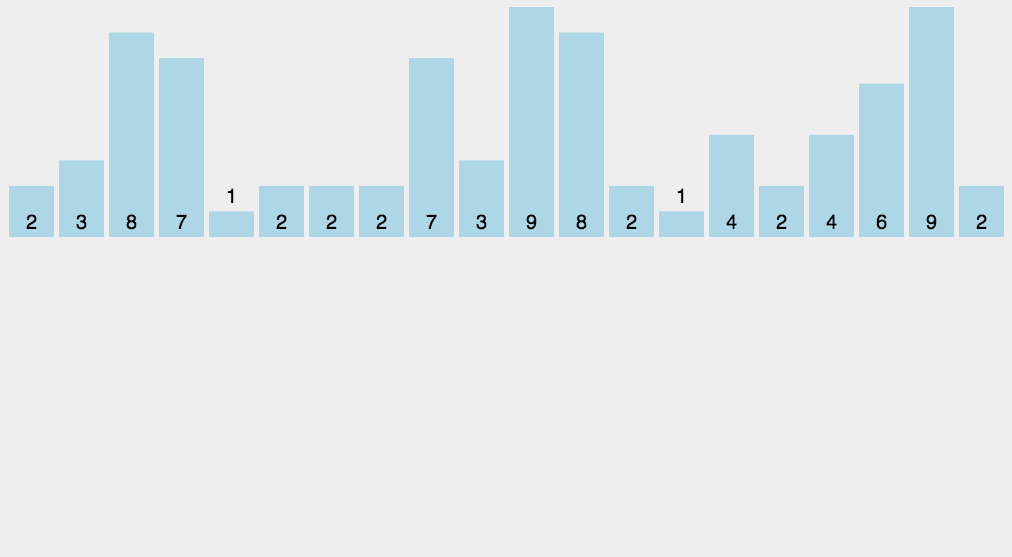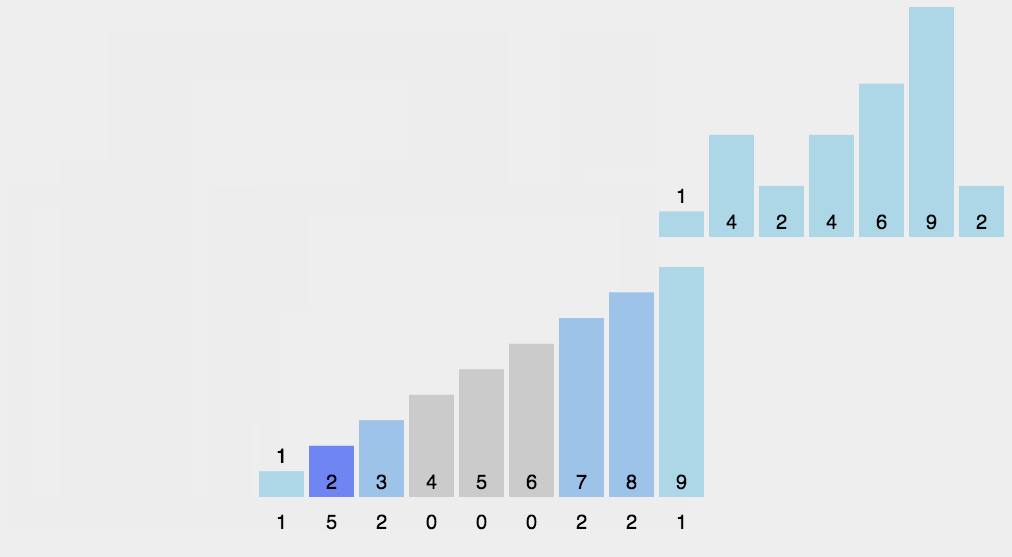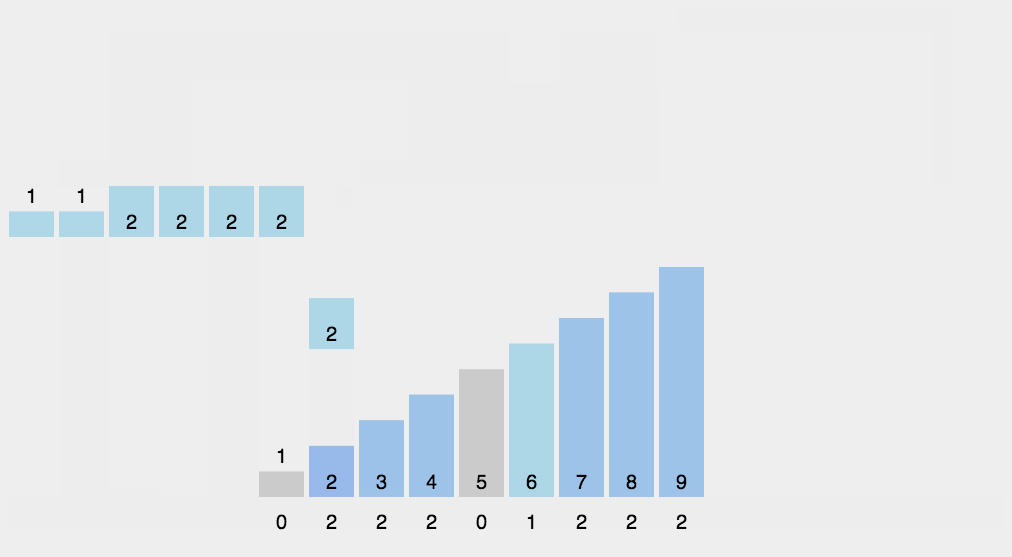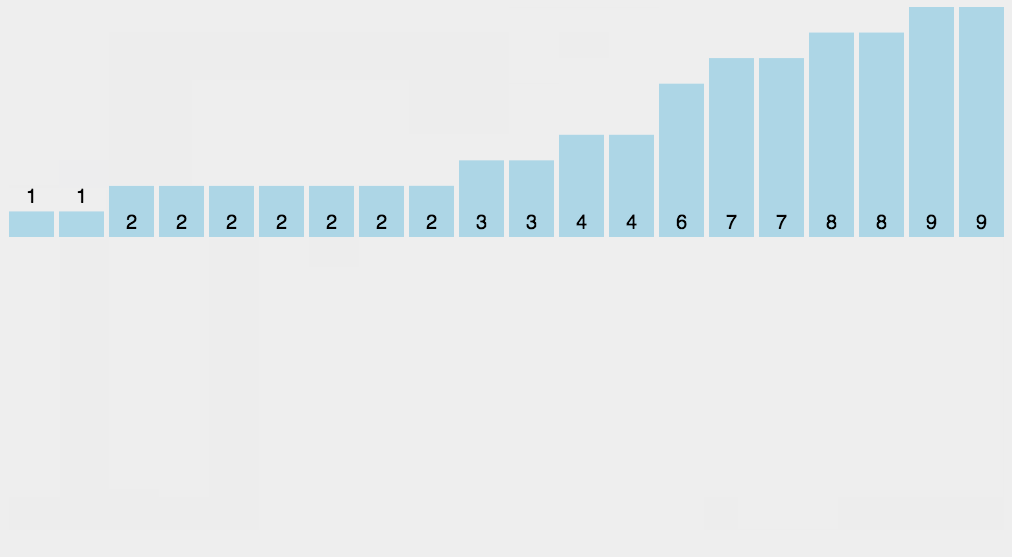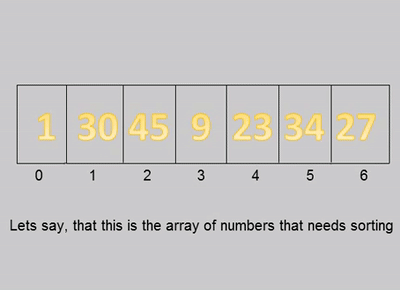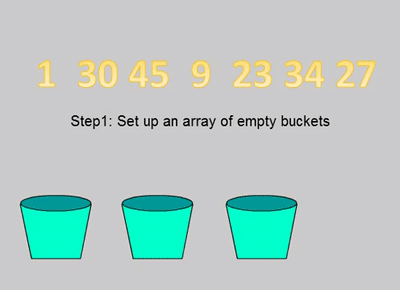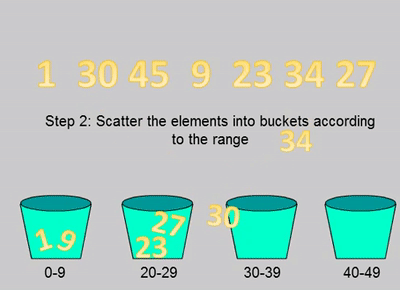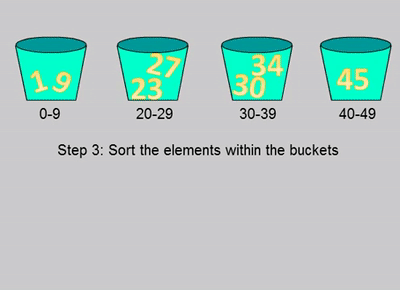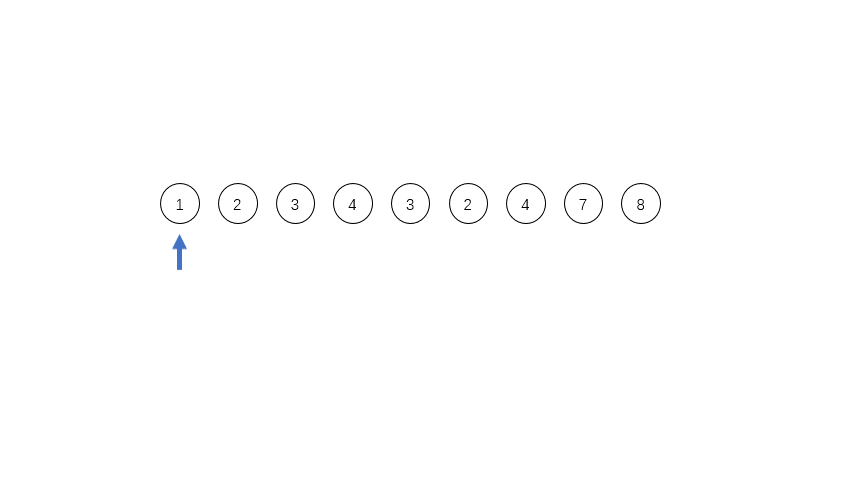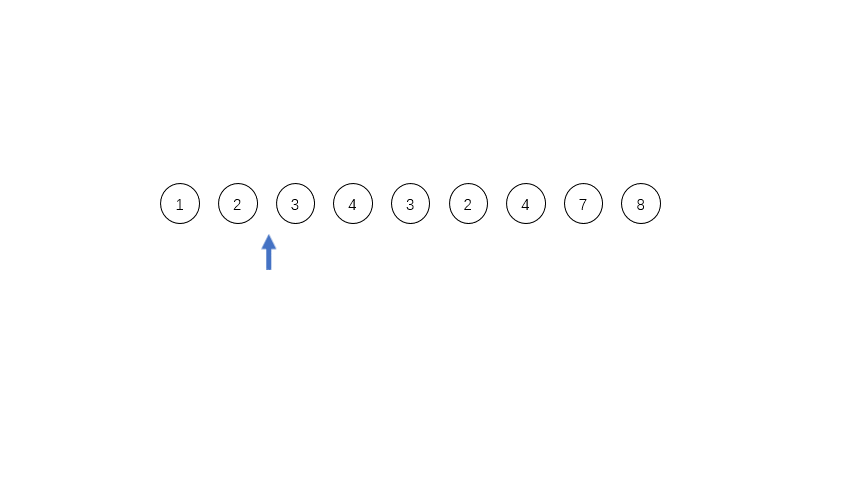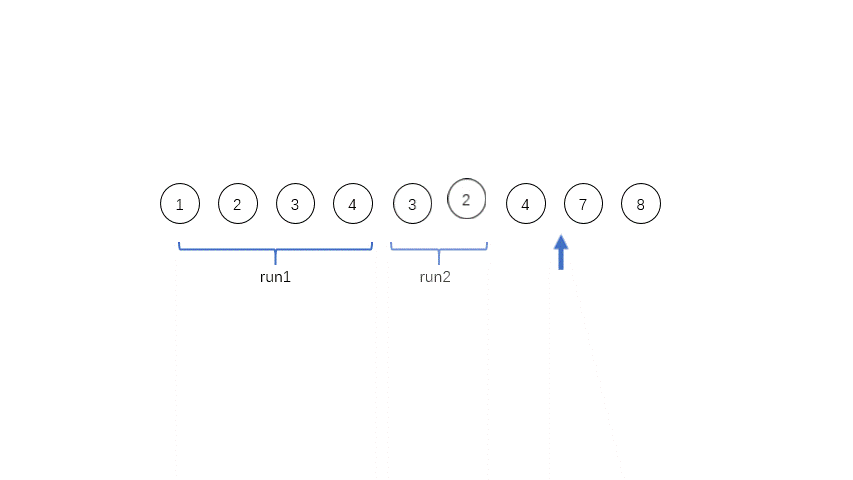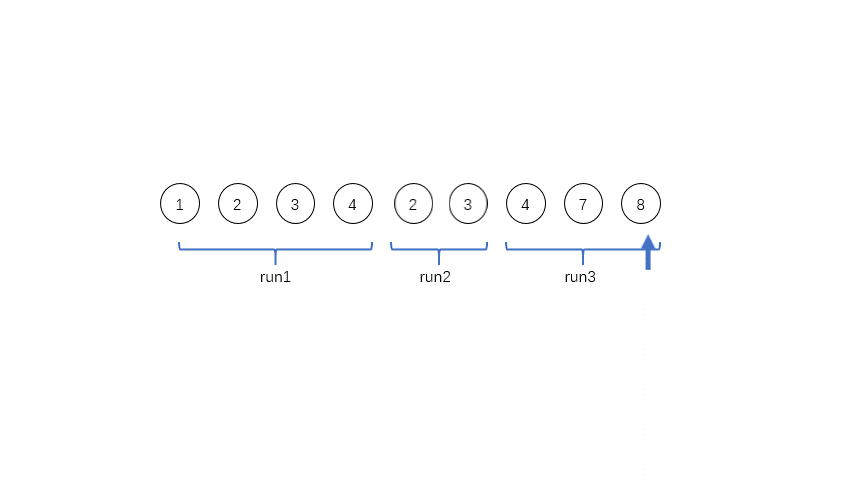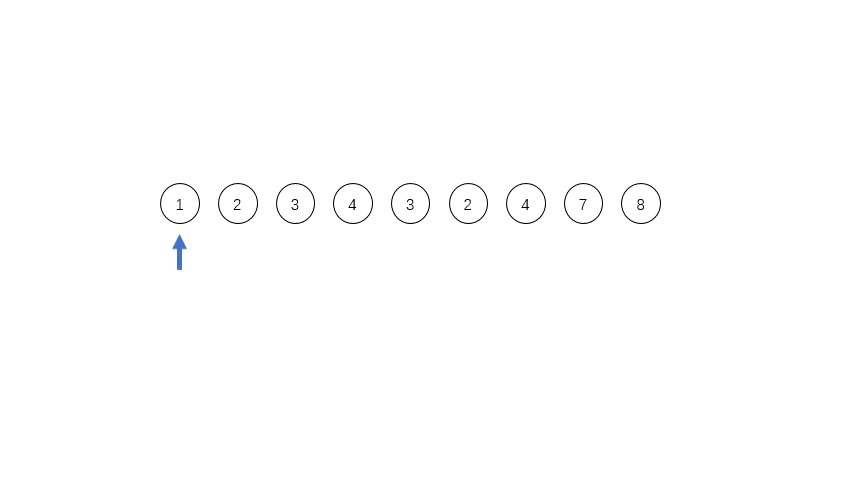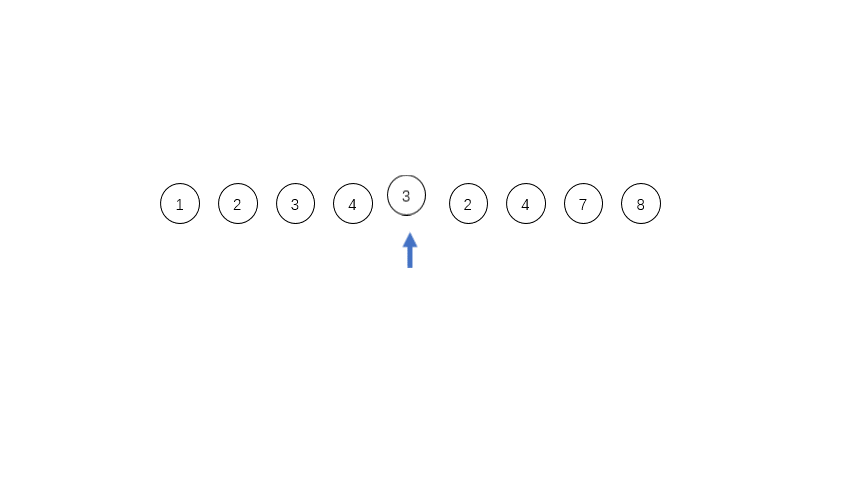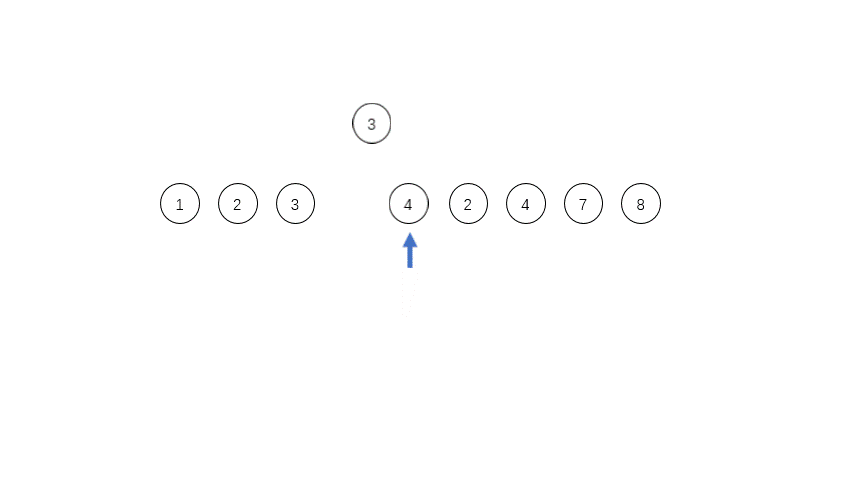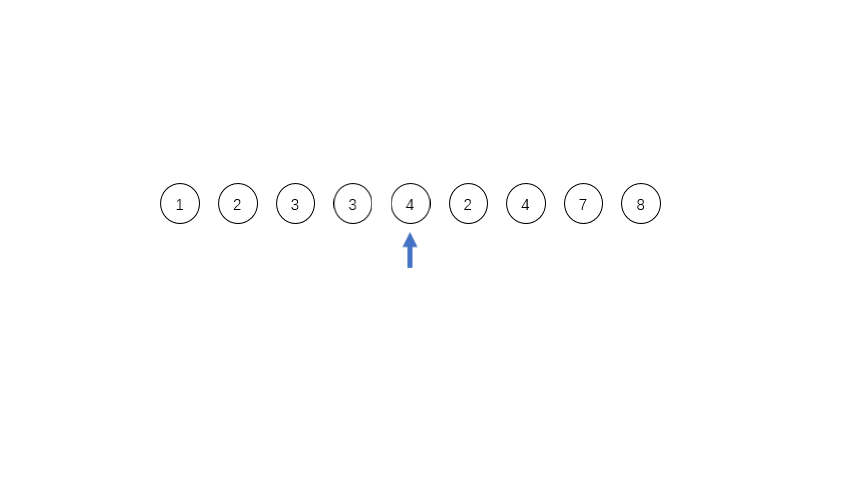排序算法全面解析
排序算法的类别和特性概览
排序算法类别
排序算法主要分为两大类:比较排序和非比较排序。
比较排序 (Comparison Sort):
这类算法通过比较元素之间的大小来确定它们的相对顺序。它们的性能上限由一个重要的数学定理决定:任何基于比较的排序算法,其最坏情况下的时间复杂度都无法低于 O(nlogn)。
主要算法包括:
冒泡排序 (Bubble Sort): 不断交换相邻的逆序元素,直到整个序列有序。
选择排序 (Selection Sort): 每次从未排序部分选择最小(或最大)的元素,放到已排序部分的末尾。
插入排序 (Insertion Sort): 每次将一个待排序的元素插入到已排序序列的正确位置。
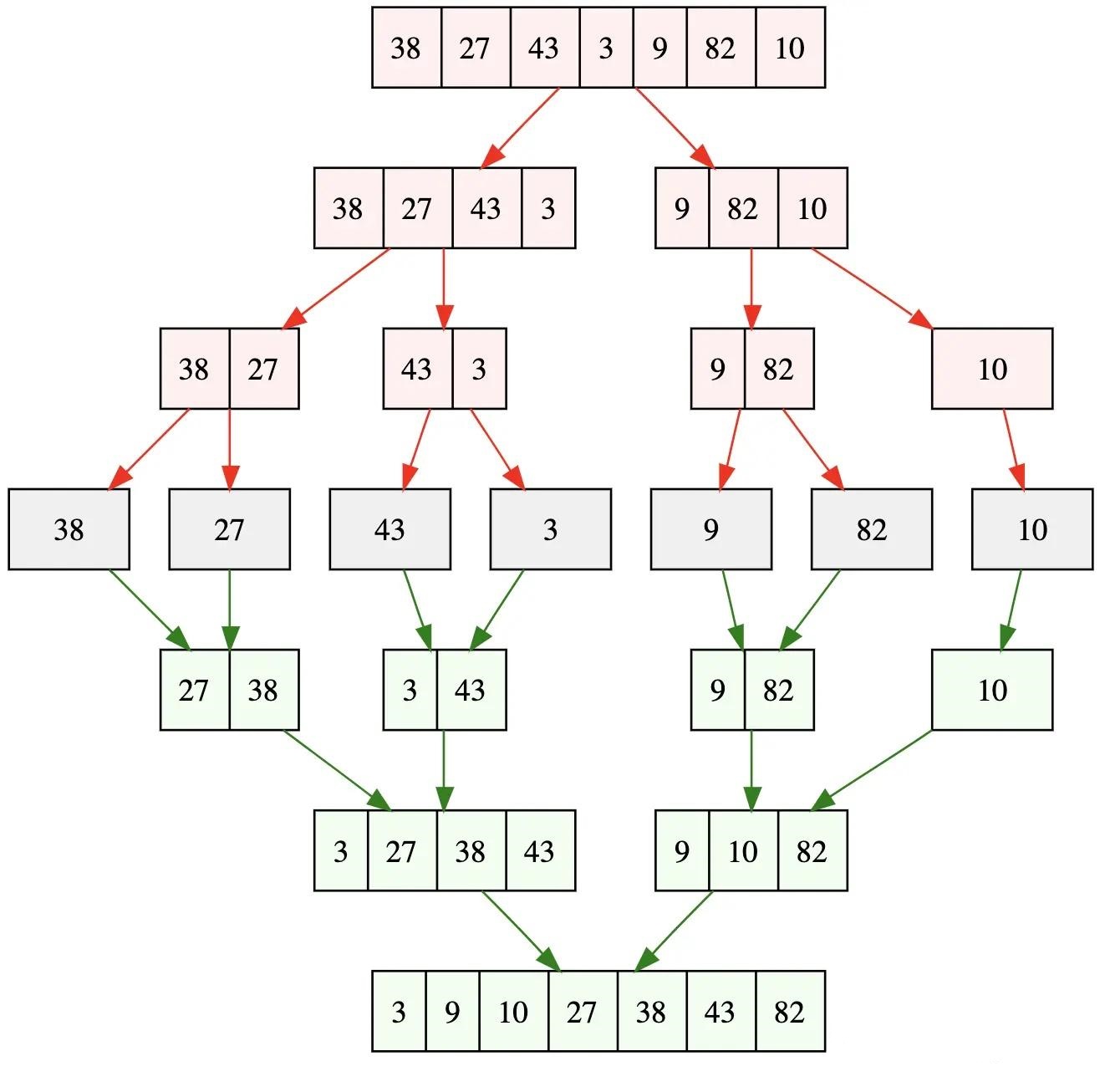
归并排序 (Merge Sort): 采用“分而治之”的思想,将序列递归地分成两半,分别排序,然后将两个有序子序列合并。
快速排序 (Quick Sort): 同样是“分而治之”,选取一个基准元素,将序列分割成两部分,一部分比基准小,另一部分比基准大,然后对这两部分递归排序。
堆排序 (Heap Sort): 利用堆这种特殊的数据结构,将序列构造成一个大顶堆(或小顶堆),然后不断将堆顶元素取出放到末尾,并重新调整堆。
非比较排序 (Non-Comparison Sort):
这类算法不依赖于元素之间的比较,而是利用其他特性(如元素的数值范围、基数等)来排序。因此,它们可以突破比较排序的 O(nlogn) 下界,在特定条件下能达到线性的时间复杂度 O(n)。
主要算法包括:
计数排序 (Counting Sort): 适用于整数排序,创建一个额外的数组来存储每个元素出现的次数,然后根据计数数组来重构有序序列。它要求待排序的数范围不能太大。
桶排序 (Bucket Sort): 将待排序的元素分配到有限数量的桶里,每个桶再单独排序(可以采用其他排序算法),最后再将所有桶中的元素依次取出。它适用于数据分布均匀的情况。
基数排序 (Radix Sort): 按照元素的位(个位、十位、百位…)从低到高(或从高到低)进行排序。它需要对整数进行处理,并且通常利用稳定的子排序算法(如计数排序)来完成每一位的排序。
排序算法稳定性
排序算法的稳定性是指,当待排序的序列中存在两个或多个相等的元素时,经过排序后,这几个相等元素在序列中的相对位置是否会发生改变。
简单来说,如果排序前后,相等元素的相对顺序保持不变,那么这个排序算法就是稳定的。反之,如果它们的相对顺序可能发生改变,那么这个算法就是不稳定的
举个例子 假设你有一组数据,其中包含两个相同的值,但它们还附带了额外的信息(例如颜色)。
- 原始序列:
(8, 蓝色),(5, 红色),(8, 绿色)
现在我们对这个序列进行排序。
如果使用稳定的排序算法,结果会是:
(5, 红色),(8, 蓝色),(8, 绿色)
两个8的相对顺序没有改变,”蓝色”的8依然在”绿色”的8前面。
如果使用不稳定的排序算法,结果可能是:
(5, 红色),(8, 绿色),(8, 蓝色)
两个8的相对顺序改变了,”绿色”的8跑到了”蓝色”的8前面。
排序算法详细对比表
| 序号 | 算法名称 | 类型 | 最低时间复杂度 | 最高时间复杂度 | 平均时间复杂度 | 空间复杂度 | 稳定性 | 备注 |
|---|---|---|---|---|---|---|---|---|
| 1 | 冒泡排序 | 比较排序 | $O(n)$ | $O(n^2)$ | $O(n^2)$ | $O(1)$ | 稳定 | |
| 2 | 选择排序 | 比较排序 | $O(n^2)$ | $O(n^2)$ | $O(n^2)$ | $O(1)$ | 不稳定 | |
| 3 | 插入排序 | 比较排序 | $O(n)$ | $O(n^2)$ | $O(n^2)$ | $O(1)$ | 稳定 | |
| 4 | 归并排序 | 比较排序 | $O(n \log n)$ | $O(n \log n)$ | $O(n \log n)$ | $O(n)$ | 稳定 | |
| 5 | 快速排序 | 比较排序 | $O(n \log n)$ | $O(n^2)$ | $O(n \log n)$ | $O(\log n)$ ~ $O(n)$ | 不稳定 | |
| 6 | 堆排序 | 比较排序 | $O(n \log n)$ | $O(n \log n)$ | $O(n \log n)$ | $O(1)$ | 不稳定 | |
| 7 | 计数排序 | 非比较排序 | $O(n+k)$ | $O(n+k)$ | $O(n+k)$ | $O(n+k)$ | 稳定 | |
| 8 | 桶排序 | 非比较排序 | $O(n+k)$ | $O(n^2)$ | $O(n+k)$ | $O(n+k)$ | 稳定 | |
| 9 | 基数排序 | 非比较排序 | $O(d \cdot (n+k))$ | $O(d \cdot (n+k))$ | $O(d \cdot (n+k))$ | $O(n+k)$ | 稳定 | |
| 10 | 二叉排序 | 比较排序 | $O(n \log n)$ | $O(n^2)$ | $O(n \log n)$ | $O(n)$ | 不稳定 | |
| 11 | Tim排序 | 混合排序 | $O(n)$ | $O(n \log n)$ | $O(n \log n)$ | $O(n)$ | 稳定 | 是目前已知最快的排序算法,在Python、Swift、Rust等语言的内置排序功能中被用作默认算法 |
| 12 | 内省排序 | 混合排序 | $O(n \log n)$ | $O(n \log n)$ | $O(n \log n)$ | $O(\log n)$ | 不稳定 | C++的默认排序算法 |
| 13 | 鸡尾酒排序 | 比较排序 | $O(n)$ | $O(n^2)$ | $O(n^2)$ | $O(1)$ | 稳定 | |
| 14 | 梳排序 | 比较排序 | $O(n \log n)$ | $O(n^2)$ | $O(n^2 / 2^p)$ | $O(1)$ | 不稳定 | |
| 15 | 希尔排序 | 比较排序 | $O(n \log n)$ | $O(n^2)$ | $O(n \log^2 n)$ | $O(1)$ | 不稳定 | |
| 16 | 原地归并排序 | 比较排序 | $O(n \log n)$ | $O(n \log n)$ | $O(n \log n)$ | $O(1)$ | 稳定 | |
| 17 | 鸽巢排序 | 非比较排序 | $O(n+k)$ | $O(n+k)$ | $O(n+k)$ | $O(n+k)$ | 稳定 | |
| 18 | 奇偶排序 | 比较排序 | $O(n)$ | $O(n^2)$ | $O(n^2)$ | $O(1)$ | 稳定 | |
| 19 | 侏儒排序 | 比较排序 | $O(n)$ | $O(n^2)$ | $O(n^2)$ | $O(1)$ | 稳定 | |
| 20 | 平滑排序 | 比较排序 | $O(n)$ | $O(n \log n)$ | $O(n \log n)$ | $O(1)$ | 不稳定 | |
| 21 | 耐心排序 | 混合排序 | $O(n \log n)$ | $O(n \log n)$ | $O(n \log n)$ | $O(n)$ | 稳定 | 需要额外的$O(n+k)$空间,也需要找到最长的递增子序列(longest increasing subsequence) |
| 22 | 图书馆排序 | 比较排序 | $O(n)$ | $O(n^2)$ | $O(n \log n)$ | $O(n)$ | 稳定 | |
| 23 | Bogo排序 | 比较排序 | $O(n)$ | $\infty$ | $O(n \cdot n!)$ | $O(1)$ | 不稳定(不实用) | 最坏的情况下期望时间为无穷。 |
| 24 | 珠排序 | 非比较排序 | $O(S)$ | $O(S)$ | $O(S)$ | $O(S)$ | 稳定(不实用) | 但需要特别的硬件 |
| 25 | 煎饼排序 | 比较排序 | $O(n)$ | $O(n^2)$ | $O(n \log n)$ | $O(1)$ | 不稳定(不实用) | 但需要特别的硬件 |
| 26 | 臭皮匠排序 | 比较排序 | $O(n^{2.7})$ | $O(n^{2.7})$ | $O(n^{2.7})$ | $O(1)$ | 不稳定(不实用) | 算法简单,但需要约$n^{2.7}$的时间 |
常见基础排序算法
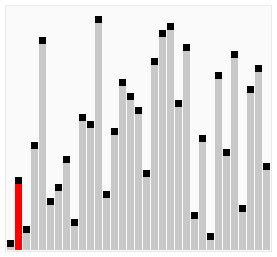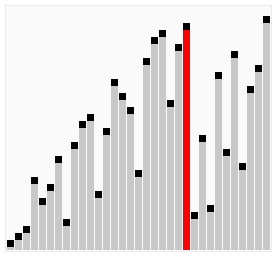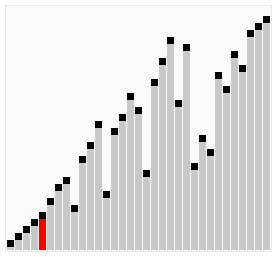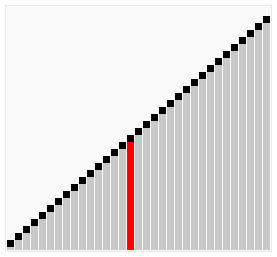
1. 冒泡排序
冒泡排序是一种简单的排序算法。它重复地走访过要排序的数列,一次比较两个元素,如果它们的顺序错误就把它们交换过来。走访数列的工作是重复地进行直到没有再需要交换,也就是说该数列已经排序完成。这个算法的名字由来是因为越小的元素会经由交换慢慢“浮”到数列的顶端。
冒泡排序规则描述
- 比较相邻的元素。如果第一个比第二个大,就交换它们两个;
- 对每一对相邻元素作同样的工作,从开始第一对到结尾的最后一对,这样在最后的元素应该会是最大的数;
- 针对所有的元素重复以上的步骤,除了最后一个;
- 重复步骤1~3,直到排序完成。
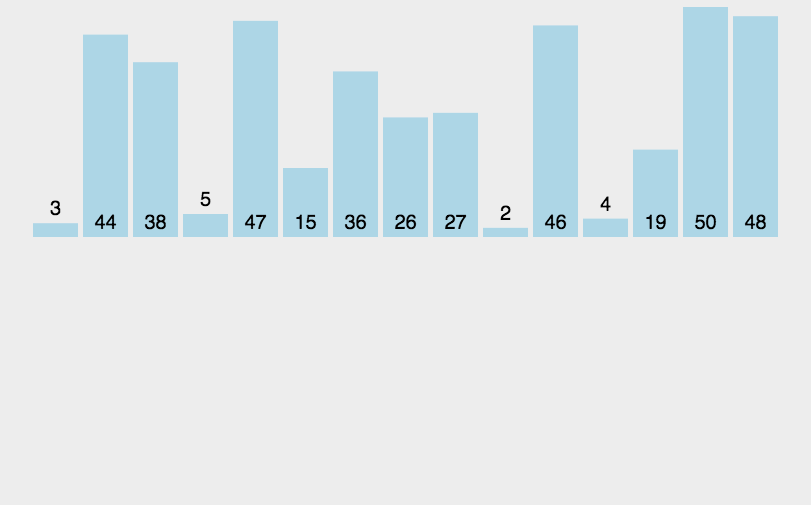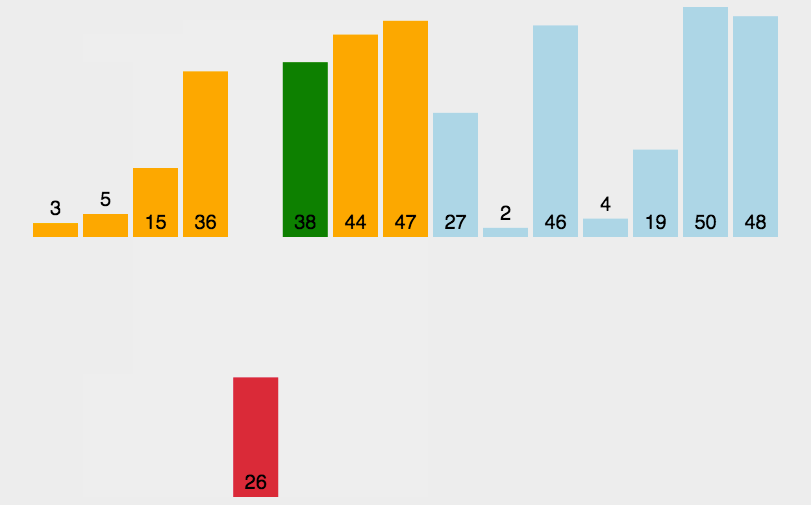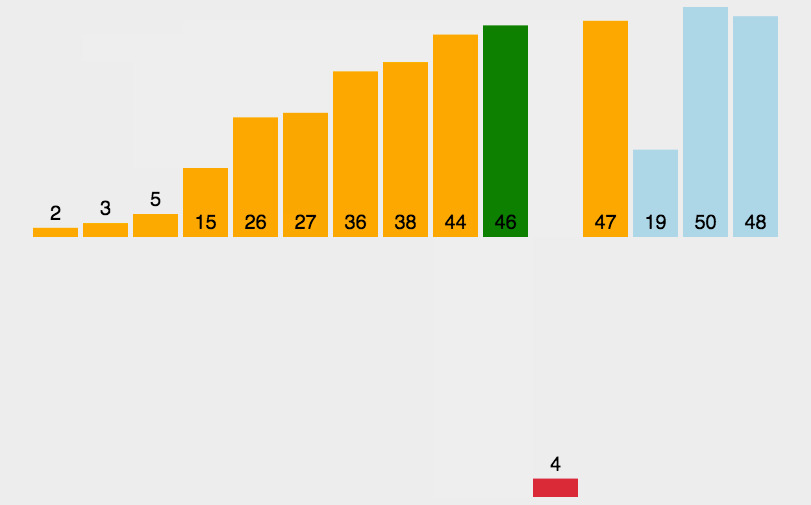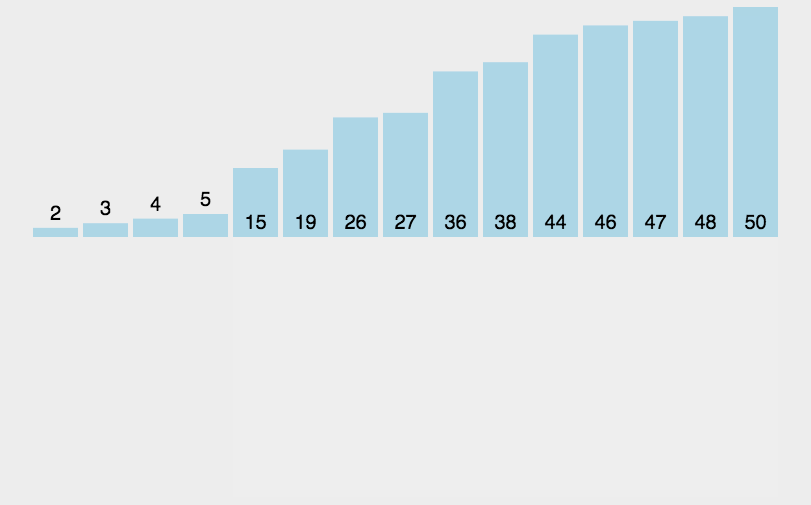
冒泡排序演示
冒泡排序示例代码
1
2
3
4
5
6
7
def bubble_sort(arr):
n = len(arr)
for i in range(n):
for j in range(0, n - i - 1):
if arr[j] > arr[j + 1]:
arr[j], arr[j + 1] = arr[j + 1], arr[j]
return arr
2. 选择排序
选择排序(Selection-sort)是一种简单直观的排序算法。它的工作原理:首先在未排序序列中找到最小(大)元素,存放到排序序列的起始位置,然后,再从剩余未排序元素中继续寻找最小(大)元素,然后放到已排序序列的末尾。以此类推,直到所有元素均排序完毕。
选择排序规则描述 n个记录的直接选择排序可经过n-1趟直接选择排序得到有序结果。具体算法描述如下:
- 初始状态:无序区为R[1..n],有序区为空;
- 第i趟排序(i=1,2,3…n-1)开始时,当前有序区和无序区分别为R[1..i-1]和R(i..n)。该趟排序从当前无序区中-选出关键字最小的记录 R[k],将它与无序区的第1个记录R交换,使R[1..i]和R[i+1..n)分别变为记录个数增加1个的新有序区和记录个数减少1个的新无序区;
- n-1趟结束,数组有序化了。
选择排序演示
选择排序示例代码
1
2
3
4
5
6
7
8
9
def selection_sort(arr):
n = len(arr)
for i in range(n):
min_idx = i
for j in range(i + 1, n):
if arr[j] < arr[min_idx]:
min_idx = j
arr[i], arr[min_idx] = arr[min_idx], arr[i]
return arr
3. 插入排序
插入排序(Insertion-Sort)的算法描述是一种简单直观的排序算法。它的工作原理是通过构建有序序列,对于未排序数据,在已排序序列中从后向前扫描,找到相应位置并插入。
插入排序规则描述 一般来说,插入排序都采用in-place在数组上实现。具体算法描述如下:
- 从第一个元素开始,该元素可以认为已经被排序;
- 取出下一个元素,在已经排序的元素序列中从后向前扫描;
- 如果该元素(已排序)大于新元素,将该元素移到下一位置;
- 重复步骤3,直到找到已排序的元素小于或者等于新元素的位置;
- 将新元素插入到该位置后;
- 重复步骤2~5。
插入排序演示
插入排序示例代码
1
2
3
4
5
6
7
8
9
def insertion_sort(arr):
for i in range(1, len(arr)):
key = arr[i]
j = i - 1
while j >= 0 and key < arr[j]:
arr[j + 1] = arr[j]
j -= 1
arr[j + 1] = key
return arr
4. 归并排序
归并排序是建立在归并操作上的一种有效的排序算法。该算法是采用分治法(Divide and Conquer)的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为2-路归并。
归并排序规则描述
- 把长度为n的输入序列分成两个长度为n/2的子序列;
- 对这两个子序列分别采用归并排序;
- 将两个排序好的子序列合并成一个最终的排序序列。
归并排序演示
归并排序示例代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
def merge_sort(arr):
if len(arr) > 1:
mid = len(arr) // 2
left_half = arr[:mid]
right_half = arr[mid:]
merge_sort(left_half)
merge_sort(right_half)
i = j = k = 0
while i < len(left_half) and j < len(right_half):
if left_half[i] < right_half[j]:
arr[k] = left_half[i]
i += 1
else:
arr[k] = right_half[j]
j += 1
k += 1
while i < len(left_half):
arr[k] = left_half[i]
i += 1
k += 1
while j < len(right_half):
arr[k] = right_half[j]
j += 1
k += 1
return arr
5. 快速排序
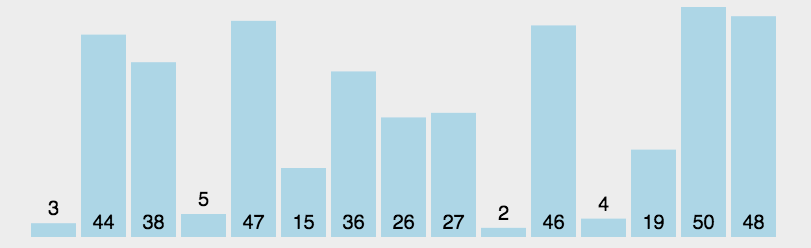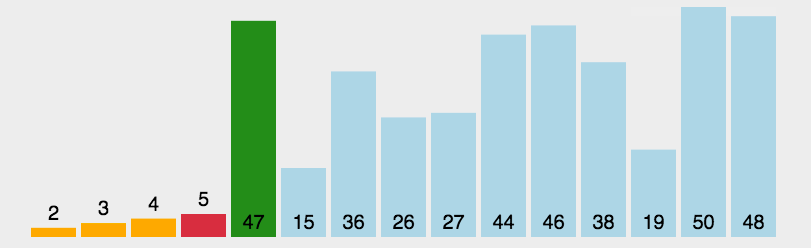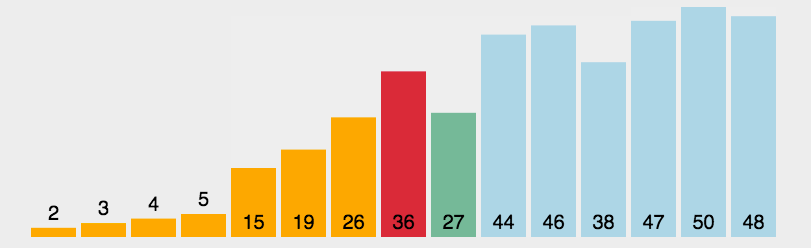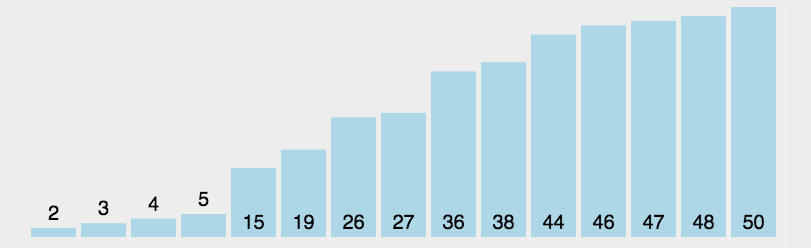
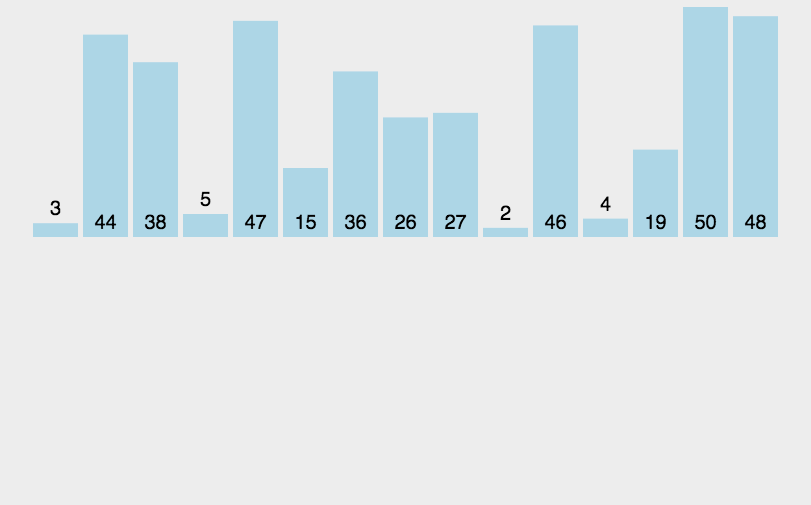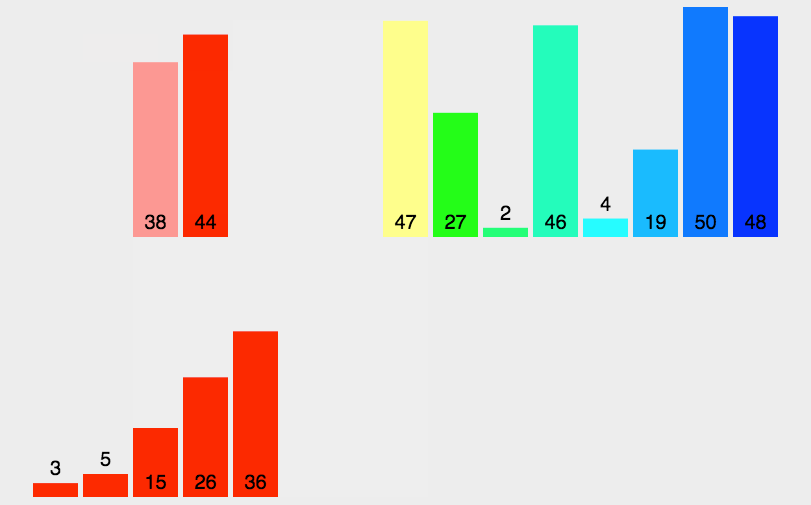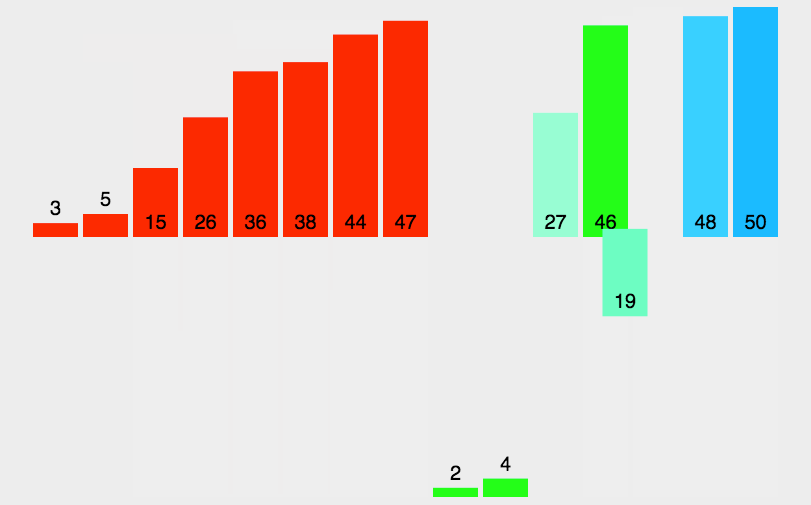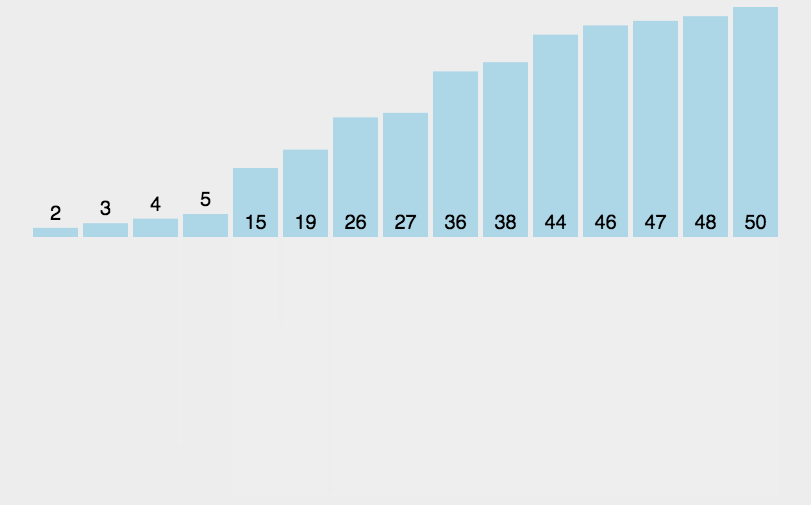
快速排序(Quick Sort)的基本思想是分而治之(Divide and Conquer) 通过一趟排序将待排记录分隔成独立的两部分,其中一部分记录的关键字均比另一部分的关键字小,则可分别对这两部分记录继续进行排序,以达到整个序列有序, 这个过程就像是在不断地“切分”数组,每次切分都能确定一个元素最终的位置,直到所有元素都找到各自的位置为止。
快速排序规则描述
- 选取基准(Pick a Pivot): 从数组中选择一个元素作为基准(pivot)。通常选择第一个、最后一个或中间的元素,也可以随机选取。
- 分区(Partition): 遍历数组,将所有小于基准的元素移到基准的左边,将所有大于基准的元素移到基准的右边。这样,基准元素就处于它最终排序后的正确位置了。
- 递归排序(Recurse): 对基准左右两侧的两个子数组重复上述步骤。当子数组的长度为1或0时,递归结束,整个数组也就完成了排序。
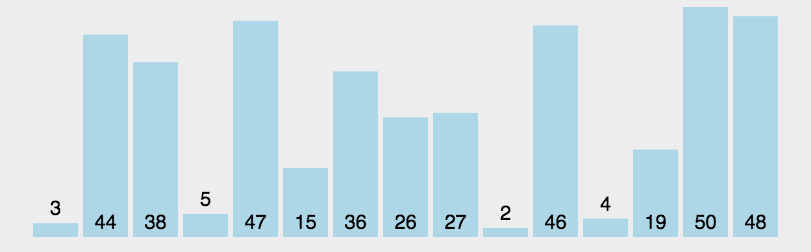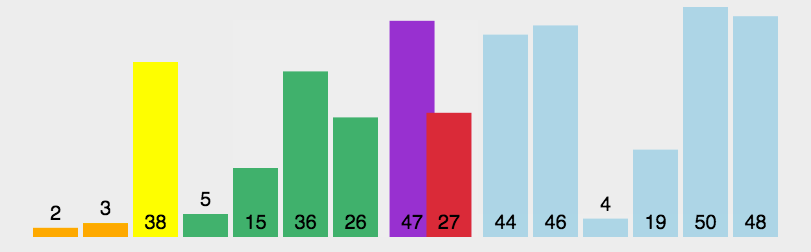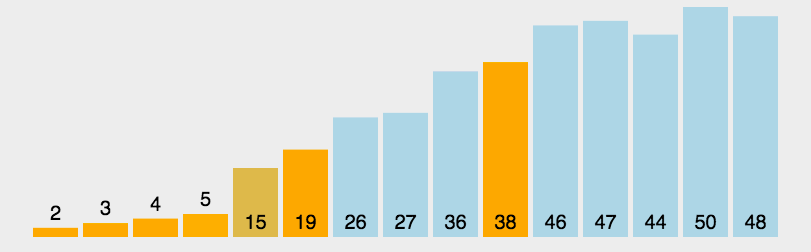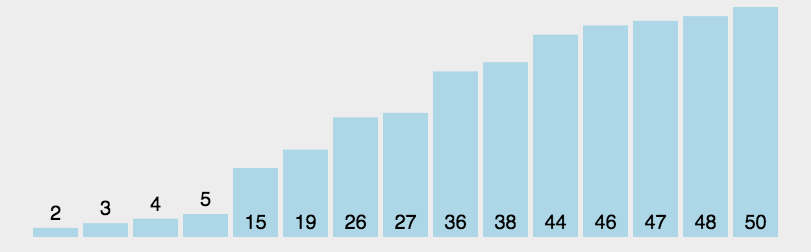
快速排序演示
快速排序示例代码
1
2
3
4
5
6
7
8
def quick_sort(arr):
if len(arr) <= 1:
return arr
else:
pivot = arr[0]
less = [i for i in arr[1:] if i <= pivot]
greater = [i for i in arr[1:] if i > pivot]
return quick_sort(less) + [pivot] + quick_sort(greater)
6. 堆排序
堆排序(Heapsort)是指利用堆这种数据结构所设计的一种排序算法。堆是一个近似完全二叉树的结构,并同时满足堆的性质:即子节点的键值或索引总是小于(或者大于)它的父节点。
堆排序规则描述
第一步:构建最大堆(或最小堆)
将待排序的数组构造成一个最大堆(如果想升序排序)。在最大堆中,每个父节点的值都大于或等于其子节点的值。构建过程从最后一个非叶子节点开始,自下而上地对所有非叶子节点进行“下沉”调整(也叫堆化),以确保每个子树都满足最大堆的性质。
第二步:重复取出堆顶元素并调整堆
构建好最大堆后,整个数组的最大值(也就是排序后的最后一个元素)就位于数组的第一个位置(堆顶)。接下来的操作循环进行,直到堆为空:
- 交换: 将堆顶元素(当前数组中的最大值)与数组的最后一个元素进行交换。这样,最大的元素就被放到了数组的末尾,即其最终的排序位置。
- 缩小堆: 将数组的有效长度减1,即把刚才交换过去的元素排除在堆之外。
- 调整: 将新的堆顶元素进行“下沉”调整,使其满足最大堆的性质。这个过程会不断地将当前堆中最大的元素“浮”到堆顶。
重复这个过程,每轮都能确定一个元素最终的排序位置,直到所有元素都按顺序放到数组的末尾,整个排序就完成了。
堆排序演示
堆排序示例代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
def heap_sort(arr):
n = len(arr)
# 第一步:构建最大堆
for i in range(n // 2 - 1, -1, -1):
heapify(arr, n, i)
# 第二步:逐一取出堆顶元素并调整
for i in range(n - 1, 0, -1):
arr[i], arr[0] = arr[0], arr[i] # 交换堆顶元素与当前末尾元素
heapify(arr, i, 0) # 调整新的堆顶元素
def heapify(arr, n, i):
largest = i # 假设根节点是最大的
left = 2 * i + 1
right = 2 * i + 2
# 如果左子节点存在且大于根节点
if left < n and arr[left] > arr[largest]:
largest = left
# 如果右子节点存在且大于目前最大的节点
if right < n and arr[right] > arr[largest]:
largest = right
# 如果最大的不是根节点,则进行交换并继续堆化
if largest != i:
arr[i], arr[largest] = arr[largest], arr[i]
heapify(arr, n, largest)
7. 计数排序
计数排序不是基于比较的排序算法,其核心在于将输入的数据值转化为键存储在额外开辟的数组空间中。 作为一种线性时间复杂度的排序,计数排序要求输入的数据必须是有确定范围的整数。通常只能应用在键的变化范围比较小的情况下,如果键的变化范围特别大,建议使用基数排序。
计数排序规则描述
- 找出待排序的数组中最大和最小的元素;
- 统计数组中每个值为i的元素出现的次数,存入数组C的第i项;
- 对所有的计数累加(从C中的第一个元素开始,每一项和前一项相加);
- 反向填充目标数组:将每个元素i放在新数组的第C(i)项,每放一个元素就将C(i)减去1。
计数排序演示
计数排序示例代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
def counting_sort(arr):
if not arr:
return []
# 找到数组中的最大值和最小值
max_val = max(arr)
min_val = min(arr)
# 确定计数数组的范围
range_of_elements = max_val - min_val + 1
count = [0] * range_of_elements
output = [0] * len(arr)
# 统计每个元素出现的次数
for num in arr:
count[num - min_val] += 1
# 计算每个元素在排序后数组中的最终位置
for i in range(1, len(count)):
count[i] += count[i - 1]
# 根据计数数组将元素放入输出数组
for i in range(len(arr) - 1, -1, -1):
output[count[arr[i] - min_val] - 1] = arr[i]
count[arr[i] - min_val] -= 1
return output
8. 桶排序
桶排序是计数排序的升级版。它利用了函数的映射关系,高效与否的关键就在于这个映射函数的确定。桶排序 (Bucket sort)的工作的原理:假设输入数据服从均匀分布,将数据分到有限数量的桶里,每个桶再分别排序(有可能再使用别的排序算法或是以递归方式继续使用桶排序进行排)
桶排序规则描述
- 设置一个定量的数组当作空桶;
- 遍历输入数据,并且把数据一个一个放到对应的桶里去;
- 对每个不是空的桶进行排序;
- 从不是空的桶里把排好序的数据拼接起来。
桶排序演示
桶排序示例代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
def bucket_sort(arr):
# 如果列表为空,直接返回空列表
if not arr:
return []
# 找到最大值,并根据数据范围创建桶
max_value = max(arr)
bucket_count = max_value + 1 # 假设元素为非负整数
buckets = [[] for _ in range(bucket_count)]
# 将元素放入桶中
for num in arr:
buckets[num].append(num)
# 收集排序后的结果
sorted_arr = []
for bucket in buckets:
# 对每个桶内的元素进行排序(这里使用Python内置的排序,也可以用其他排序算法)
for item in sorted(bucket):
sorted_arr.append(item)
return sorted_arr
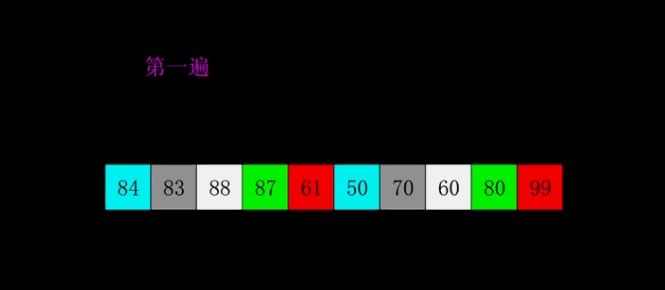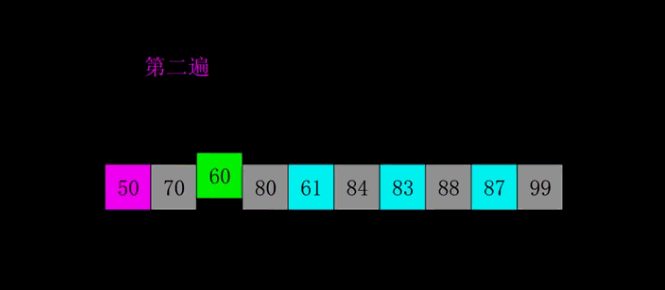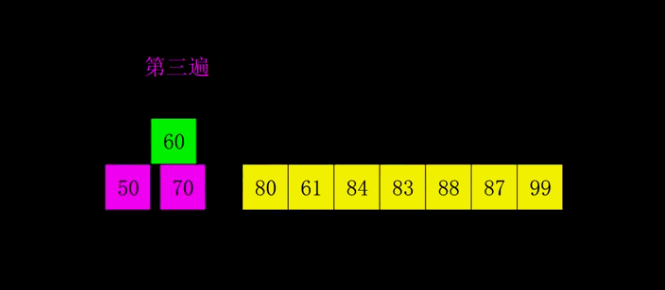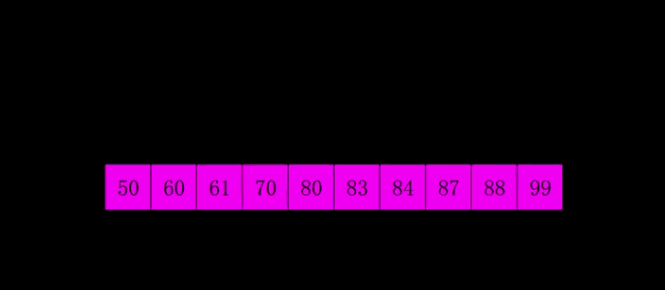
9. 基数排序
基数排序是按照低位先排序,然后收集;再按照高位排序,然后再收集;依次类推,直到最高位。有时候有些属性是有优先级顺序的,先按低优先级排序,再按高优先级排序。最后的次序就是高优先级高的在前,高优先级相同的低优先级高的在前。
基数排序规则描述
- 取得数组中的最大数,并取得位数;
- arr为原始数组,从最低位开始取每个位组成radix数组;
- 对radix进行计数排序(利用计数排序适用于小范围数的特点);
基数排序演示
基数排序示例代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
def counting_sort_for_radix(arr, exp):
"""
用于基数排序的计数排序,按 exp 位进行排序。
exp 代表当前的位数,例如 1, 10, 100, ...
"""
n = len(arr)
output = [0] * n
count = [0] * 10 # 因为数字的每一位都在 0-9 之间
# 统计每个数字在当前位出现的次数
for i in range(n):
index = (arr[i] // exp) % 10
count[index] += 1
# 将 count 转换为累积次数,以确定元素在输出数组中的位置
for i in range(1, 10):
count[i] += count[i - 1]
# 从后向前遍历,将元素放入输出数组,确保稳定性
i = n - 1
while i >= 0:
index = (arr[i] // exp) % 10
output[count[index] - 1] = arr[i]
count[index] -= 1
i -= 1
# 将输出数组的内容复制回原数组,以便进行下一位的排序
for i in range(n):
arr[i] = output[i]
def radix_sort(arr):
"""
基数排序主函数
"""
if not arr:
return []
# 找到最大值,以确定排序的位数
max_val = max(arr)
# 从个位(exp=1)开始,逐位进行计数排序
exp = 1
while max_val // exp > 0:
counting_sort_for_radix(arr, exp)
exp *= 10
return arr
10. 二叉排序
二叉排序,也称为树排序,是一种利用二叉搜索树(Binary Search Tree,简称 BST)数据结构来完成排序的算法
二叉搜索树(binary search tree,简称BST)[a]是一种有根二叉树数据结构。它要求每个内部节点的键值都大于其左子树中所有节点的键值,且都小于其右子树中所有节点的键值。该树各项操作时间复杂度均与树的高度成线性关系。
二叉排序的核心优势在于它将排序问题转化为一个数据结构问题。然而,由于它在最坏情况下性能会急剧下降,因此在实际应用中,通常会使用平衡二叉搜索树(如 AVL 树、红黑树)来代替普通的二叉搜索树,以确保无论数据如何,其时间复杂度都能稳定保持在 $O(n \log n)$
二叉排序规则描述
- 构建二叉搜索树:
- 遍历待排序的数组,将每一个元素依次插入到一个空的二叉搜索树中。
- 二叉搜索树的特性是:对于任意一个节点,其左子树中的所有节点的值都小于它,而右子树中的所有节点的值都大于它。
- 中序遍历:
- 在树构建完成后,对这棵二叉搜索树进行中序遍历(in-order traversal)。
- 中序遍历的顺序是:先递归遍历左子树,然后访问根节点,最后递归遍历右子树。
- 由于二叉搜索树的特性,其中序遍历的结果就是所有节点的一个有序序列。
二叉排序示例代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
class TreeNode:
def __init__(self, value):
self.value = value
self.left = None
self.right = None
class BinarySortTree:
def __init__(self):
self.root = None
def insert(self, value):
if self.root is None:
self.root = TreeNode(value)
else:
self._insert_recursively(self.root, value)
def _insert_recursively(self, node, value):
if value < node.value:
if node.left is None:
node.left = TreeNode(value)
else:
self._insert_recursively(node.left, value)
else:
if node.right is None:
node.right = TreeNode(value)
else:
self._insert_recursively(node.right, value)
def inorder_traversal(self, node):
result = []
if node:
result.extend(self.inorder_traversal(node.left))
result.append(node.value)
result.extend(self.inorder_traversal(node.right))
return result
def tree_sort(arr):
if not arr:
return []
bst = BinarySortTree()
for item in arr:
bst.insert(item)
return bst.inorder_traversal(bst.root)
多种基础排序算法的组合
11. Tim排序
Timsort是由Tim Peters在2002年实现的,自Python 2.3以来,它一直是Python的标准排序算法。Java在JDK中使用Timsort对非基本类型进行排序。Android平台和GNU Octave还将其用作默认排序算法。
Timsort是一种稳定的混合排序算法,同时应用了二分插入排序和归并排序的思想,在时间上击败了其他所有排序算法。它在最坏情况下的时间复杂度为 $O(nlogn)$ 优于快速排序;最佳情况的时间复杂度为 $ O(n) $ ,优于归并排序和堆排序。由于使用了归并排序,使用额外的空间保存数据,TimSort空间复杂度是 $ O(n) $
Tim排序中特殊概念定义
Run: TimSort 的核心思想是利用真实世界数据中通常存在的部分有序性。它不是盲目地对整个数组进行排序,而是首先寻找和识别数据中已有的“自然排序子序列(natrue run)”,也叫run。一个
run是指一个连续的、单调递增或单调递减的子序列。例如,在数组[1, 2, 5, 8, 4, 3, 9, 10]中,[1, 2, 5, 8]和[3, 9, 10]都是run。MIN_RUN: 在 Timsort 算法中,run 的生成非常关键,而这一过程的核心是确定 run 最小长度 minrun。这个长度的设定是为了在排序过程中达到两个关键目标:- 确保 run 足够长,以便有效地利用归并排序;
- 避免 run 过于长,从而在合并时仍能保持高效。 实验研究表明,当 minrun 小于 8 时,第一条原则难以满足;而当 minrun 超过 256 时,第二条原则受到影响。
因此,最佳的 minrun 长度范围被确定在 32 到 64 之间。
这个范围与我们之前提到的插入排序中小规模数据集的长度范围非常接近,这并非巧合。事实上,Timsort 在生成
run时也会利用到插入排序。具体计算 minrun 的方法如下:
- 目标:选取一个 minrun 值,以使长度为 n 的数组被分割成约 $n/minrun$ 个 runs,每个
run包含大约 32 到 64 个元素。 - 计算方法:选择最接近 $n/(2^k)$ 的 minrun 值,这里 k 是使 $n/(2^k)$ 落在32至64之间的最大整数。然后设置 minrun 为 $n/(2^k)$。
例如,对于长度为 65 的数组,minrun 将设置为33,形成 2 个runs;对于长度为 165 的数组,minrun 设置为42,形成 4 个runs。
这个计算过程涉及到 (2^k),可以通过位移操作高效实现:
GALLOP: GALLOP 模式(Galloping Mode)是 TimSort 算法在合并(merge)阶段的一个关键优化机制。它的目的是为了应对一种特殊情况:当一个run的所有元素都远小于另一个run的所有元素时,可以大大减少比较次数。GALLOP搜索元素分为两个步骤,比如我们想找到A中的元素x在B中的位置
是在B中找到合适的索引区间 $(2^k−1,2^{k+1}−1)$ 使得x在这个元素的范围内
是在第一步找到的范围内通过二分搜索来找到对应的位置。
通过这种搜索方式搜索序列B最多需要 $2lgB$ 次的比较,相比于直接进行二分搜索的 $lg(B+1)$ 次比较,在数组长度比较短或者重复元素比较多的时候,这种搜索方式更加有优势。
这个搜索算法又叫做指数搜索(exponential search),在Peter McIlroy于1993年发明的一种乐观排序算法中首次提出的。
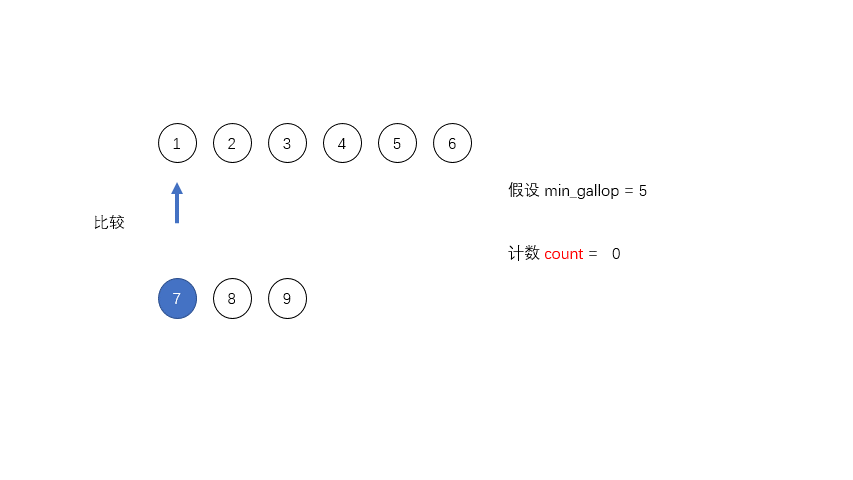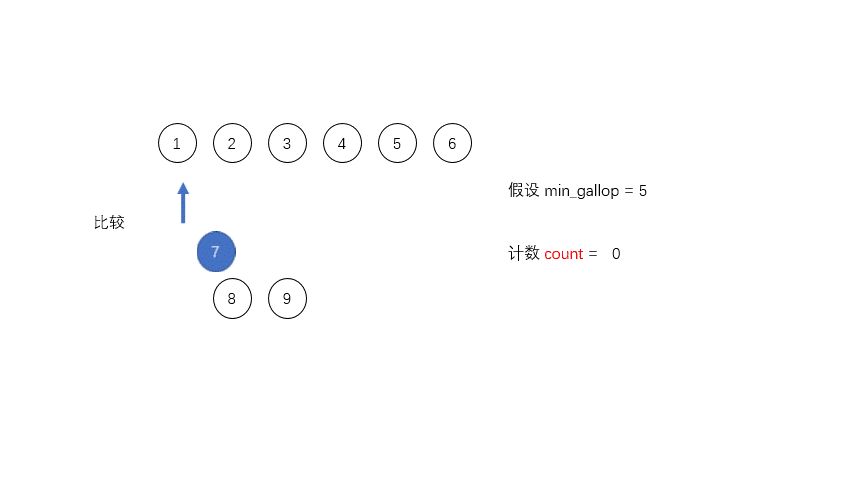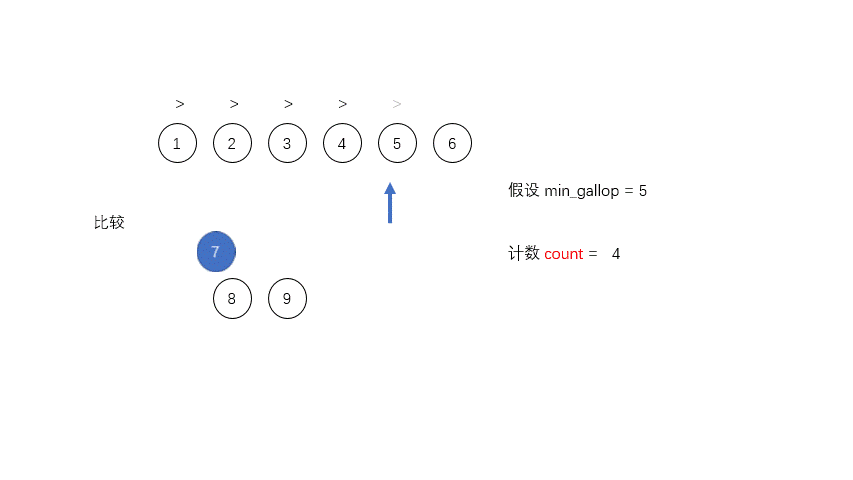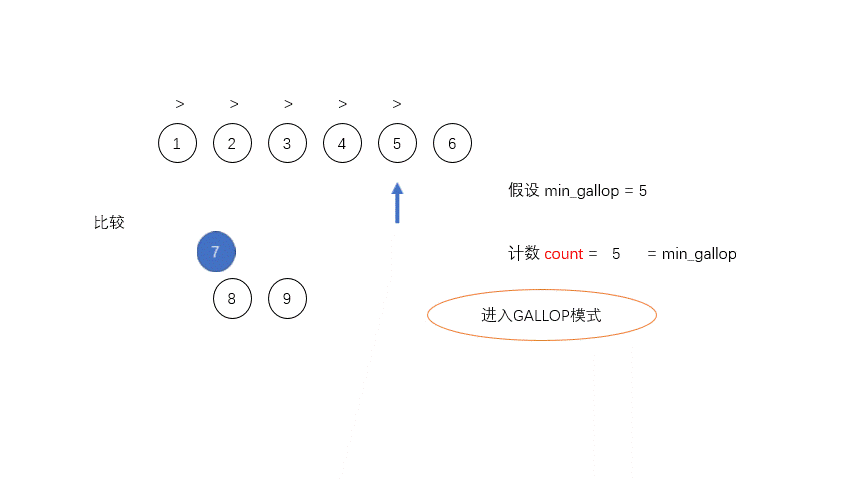
MIN_GALLOP: MIN_GALLOP 是为了优化合并的过程设定的一个阈值,控制进入 GALLOP 模式中在归并排序算法中合并两个数组就是一一比较每个元素,把较小的放到相应的位置,然后比较下一个,这样有一个缺点就是如果
A中如果有大量的元素A[i...j]是小于B中某一个元素B[k]的,程序仍然会持续的比较A[i...j]中的每一个元素和B[k],增加合并过程中的时间消耗。为了优化合并的过程,Tim设定了一个阈值
MIN_GALLOP,如果A中连续MIN_GALLOP个元素比B中某一个元素要小,那么就进入GALLOP模式,反之亦然。默认的MIN_GALLOP值是7。MIN_MERGE: 这是个常数值,可以简单理解为执行归并的最小阀值,如果整个数组长度小于它,就没必要执行那么复杂的Tim排序,直接二分插入就行了。在 Tim Peter 的 C 实现中为 64,但实际经验中设置为 32 效果更好,所以 java 里面此值为 32。
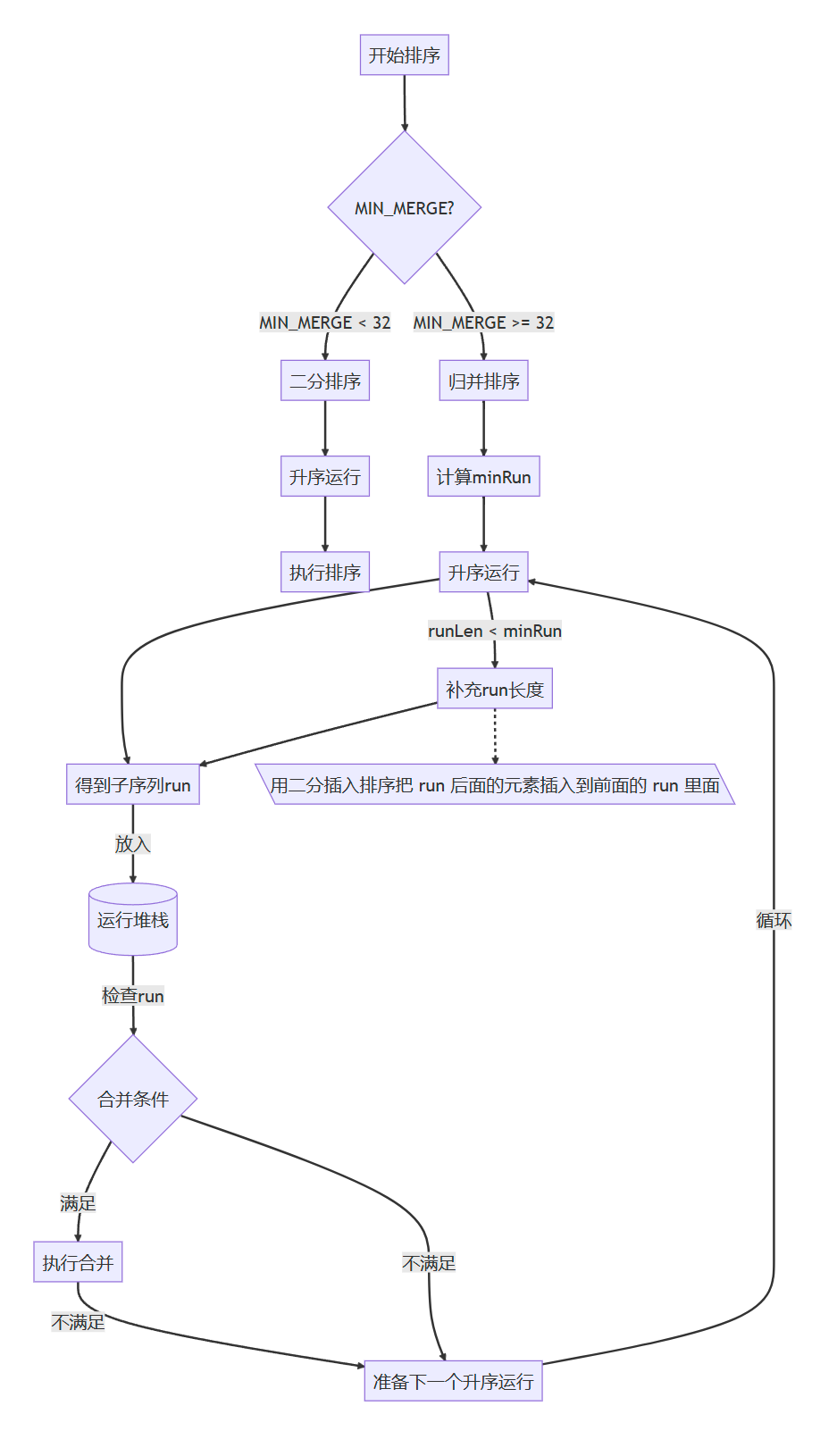
Tim排序流程描述
TimSort 的工作流程可以分为两个主要阶段:
- 判断需要排序的序列长度是否大于MIN_MERGE (实际实现中, 理论定义中不包含这个步骤)
- 序列长度小于MIN_MERGE没必要执行复杂的TimSort的归并排序部分
- 直接对序列执行二分插入排序
- 识别并排序小块(Runs):
- TimSort 会遍历数组,找到所有的“run”。
- 如果一个“run”的长度小于一个预设的最小长度(通常为 32 或 64),它会使用插入排序来对其进行排序。这是因为插入排序在处理小规模数据时非常高效。
- 如果一个“run”是递减的,TimSort 会将其反转,使其变为递增的。
- 如果“run”的长度小于minrun, 则run会在扩展后排序 (使用二分插入排序)
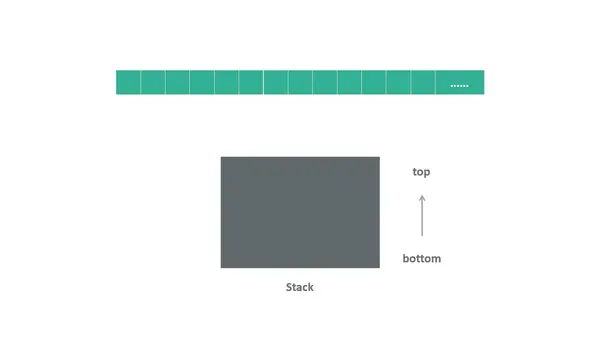
- 合并(Merge):
- 将这些已排序的“run”推入一个栈中。
- TimSort 会智能地从栈中取出相邻的“run”,使用归并排序的思想将它们合并成更大的、已排序的序列。它有一套复杂的规则来决定何时合并,以确保合并操作是高效的,并保持堆栈上的“run”长度平衡。
在算法的执行过程中,它遍历数据集,最大限度地利用在绝大多数实际数据中已经存在的连续有序序列, 借助于这些自然序列,必要时将附近的元素添加进去,形成一个个的数据块 run,其中每个 run 中的元素都会进行排序。
随后,这些有序的 run 被堆叠在一个栈中,形成了算法处理过程的一个关键结构。
当一个新的 run 被识别并加入到栈中后,Timsort 会根据栈顶多个 run 的长度来判断,是否应该合并栈顶附近的 run。
这个过程将持续进行,直到所有数据都遍历完。
遍历结束后,栈中剩余的所有 run 每次两两合并,直到最终形成一个完整有序的 run。
相比传统归并排序,合并预排序的 run 会大大减少了所需的比较次数,从而提升了整体的排序效率。
Tim排序中的特殊处理细节
Run 的生成过程
Timsort 的核心目标是充分利用数据中已存在的连续有序序列来生成
run,但这是如何实现的呢?Timsort 的处理流程中生成
run的部分可分为以下几个关键步骤:- Timsort 开始扫描整个数组,寻找连续的升序或降序序列。
- 如果遇到升序部分,Timsort 会持续扫描直到升序结束。
- 如果遇到降序部分,Timsort 会继续扫描直到降序结束,并随后将这部分翻转成升序。
如果上述步骤识别的
run未达到minrun长度,Timsort 会继续扩展这个 run,向数组后方遍历,纳入更多元素,直至达 minrun 长度。在这个阶段,新加入元素的顺序并不重要。一旦扩展完成,这个扩展后的
run(无论其最初是否有序)都将通过插入排序进行排序,以确保其内部有序。如果识别的
run长度远超minrun,对于这些较长的连续有序序列,Timsort 会保持其原始长度,不进行切割。这是因为较长的有序序列对于减少后续合并操作的复杂度非常有利。对于这些超长的
run,通常无需进行额外排序,除非它们是降序,这时 Timsort 会先将其翻转成升序。通过这些策略,Timsort 能够高效地生成一个有序的、长度至少为
minrun的run,为后续的归并排序过程奠定了坚实基础。案例: 比如对于序列
[1,2,3,4,3,2,4,7,8],其中有三个run,第一个是[1,2,3,4],第二个是[3,2],第三个是[4,7,8],这三个run都是单调的,在实际程序中对于单调递减的run会被反转成递增的序列。在合并序列的时候,如果
run的数量等于或者略小于2的幂次方的时候,效率是最高的;如果略大于2的幂次方,效率就会特别低。所以为了提高合并时候的效率,需要尽量控制每个run的长度,定义一个minrun表示每个run的最小长度,如果长度太短,就用二分插入排序把run后面的元素插入到前面的run里面。对于上面的例子,如果minrun=5,那么第一个run是不符合要求的,就会把后面的3插入到第一个run里面,变成[1,2,3,3,4]。栈中 Run 的合并规则
在 Timsort 算法中,每生成一个新的
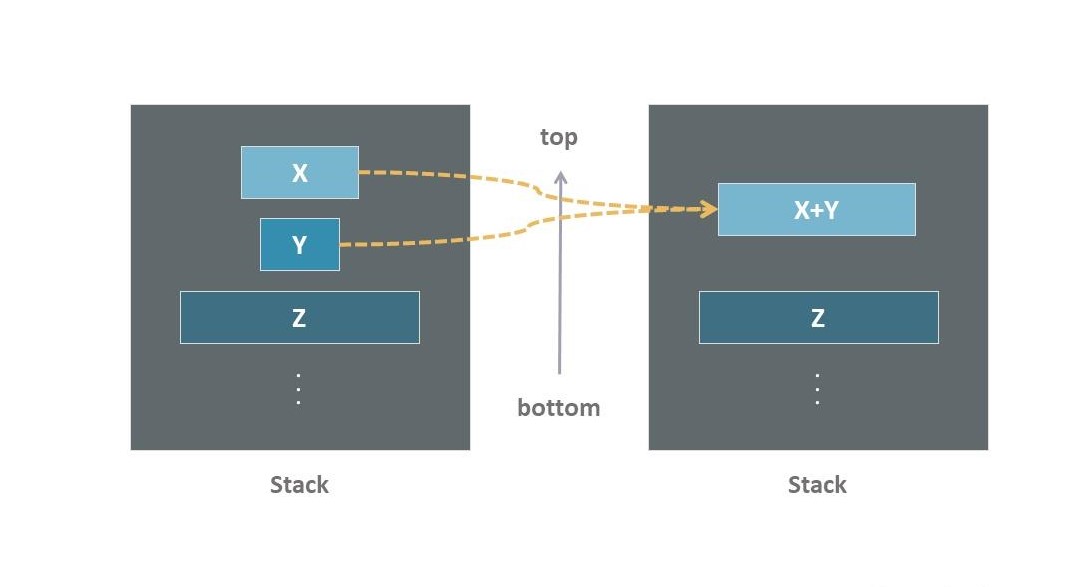
run,它就会被加入到一个专门的栈中。这时,Timsort 会对栈顶的三个
run(我们称它们为X、Y和Z)进行检查,以确保它们符合特定的合并规则:- $Z>Y+X$
- $Y>X$
如果这些条件没有被满足,Y 就会与 X 或 Z 中较小的一个合并,并重新检查上述条件。当所有条件都满足时,可以在数据中继续遍历生成新的
run。这种独特的合并规则是为了实现什么目标呢?
在 Timsort 的合并规则下,最终保留在栈中的每个
run的长度至少等于前两个run的总长度(由于满足 $Z > Y + X$ 和 $Y > X$ 的规则)。这种设计意味着,随着时间的推移,栈中
run的长度会逐渐增大,其增长方式类似于斐波那契数列。这种增长模式的一个重要优势在于,它提供了一种有效的方式来平衡数据遍历完成之后
run的合并操作,同时避免了过于频繁的合并。所有的
run每次两两合并,最终仅留下一个完整的有序run。相较于传统的 mergesort,合并预排序的run的好处是它大大降低了完成整体排序所需的比较次数。在最理想情况下,这个栈从顶部到底部
run的长度应该是[2,2,4,8,16,32,64,…]。这样,从栈顶到栈底的合并过程中,每次合并的两个run的长度都是相等的,形成了完美的合并, 如下图所示。为什么插入排序和归并排序适合处理真实世界的数据?
让我们首先探讨第一个问题,为什么插入排序成为了 Timsort 的关键组成部分。
尽管插入排序的理论时间复杂度为 $O(n^2)$,看似不及 $O(nlogn)$ 的高效排序算法,但插入排序的实际效率却非常高效,尤其是在处理小规模数据集时。
这是因为插入排序只涉及两个简单操作:比较和移动。
通过比较,我们能够确定新元素的插入点;通过移动,我们为新元素的插入腾出空间。
关键在于,对于小数据集而言,$n^2$ 与 $nlogn$ 的差异并不显著,复杂度不占主导作用,此时每轮单元的操作数量才起到决定性因素。 得益于其简洁的操作,插入排序在小规模数据集上的表现通常非常出色。
但究竟什么规模的数据集算是“小”呢?
以 Python 为例,当数据集大小小于 64 时,它会默认采用插入排序。而在 Java 中,这一界限则被设定在了 32。
插入排序的进一步优化:二分插入排序
对于 Timsort 算法来说,传统插入排序也存在进一步提升性能的空间。
回顾一下,插入排序涉及的关键操作有两个:比较和移动。这其中,对于一个数组来说,移动的总次数是固定不变的,因此,我们可以尝试从减少比较的次数来优化。
在插入排序的执行过程中,数据被划分为已排序和未排序的两个部分。在已排序部分,我们寻找未排序部分下一个元素的插入位置时,常规做法是采用线性查找。
但 Timsort 采用了更高效的策略——二分查找法。利用二分查找在已排序部分寻找插入点,大幅减少了比较次数。
对小规模数据集而言,这种优化尤其有效,能显著提升排序的效率。
Run 合并加速的 GALLOP 模式
在归并排序过程中,通常的做法是逐个比较两个数组中的元素,并将较小的元素依次放置到合适的位置。
然而,在某些情况下,这种方法可能涉及大量冗余的比较操作,尤其是当一个数组中的元素连续地胜出另一个数组时。
想象一下,如果我们有两个极端不平衡的数组:
A = [1, 2, 3, …, 9999, 10000]B = [20000, 20001, …, 29999, 30000]在这种情况下,为了确定 B 中元素的正确插入点,我们需要进行高达 10000 次的比较,这无疑是低效的。
如何解决这个问题呢?
Timsort 的解决方案是引入了所谓的“跃进模式”(galloping mode)。这种模式基于一个假设:如果一个数组中的元素连续胜出另一个数组中的元素,那么这种趋势可能会持续下去。
- Timsort 会统计从一个数组连续选中的元素数量,一旦连续胜出次数达到了称为
min_gallop的阈值时,Timsort 就会切换到跃进模式。 - 在这种模式下,算法将不再逐个比较元素,而是将实施一种指数级搜索(exponential search)。以指数级的步长 $(2^k)$ 进行跳跃,首先检查位置 1 的元素,然后是位置 3 $(1 + 2^1 )$,接着是位置 7 $(3 + 2^2)$,以此类推。
- 当首次找到大于或等于比较元素的位置时,我们就将搜索范围缩小到上一步的位置 $(2^(k-1) + 1)$ 和当前步的位置 $(2^k + 1)$ 之间的区间。
- 在这个区间内进行更二分搜索,以快速定位正确的插入位置。
据开发者的基准测试,只有当一个数组的首元素并不处于另一数组的前 7 位置时,跃进模式才真正带来优势,因此
min_gallop的阈值为 7。虽然跃进模式在某些情况下能极大提高效率,但它并非总是最优选择。有时,跃进模式可能导致更多的比较操作,尤其是在数据分布较为均匀时。
为了避免这种情况,Timsort采用了两种策略:一是当识别到跃进模式的效率不及二分搜索时,会退出跃进模式;二是根据跃进模式的成功与否调整
min_gallop值。如果跃进模式成功且连续选择的元素均来自同一数组,
min_gallop值会减 1,以鼓励再次使用跃进模式;反之,则加 1,减少再次使用跃进模式的可能性。- Timsort 会统计从一个数组连续选中的元素数量,一旦连续胜出次数达到了称为
Run 合并过程中的空间开销优化
虽然传统的归并排序也拥有 $O(nlogn)$ 的时间复杂度,但它并不是原地排序,并且需要额外的 $O(n)$ 空间开销,这使得它并没有被广泛地运用。
当然,也有改良过的原地归并排序的实现,但它们的时间开销就会比较大。为了在效率和空间节约之间取得平衡,Timsort 采用了一种改进的归并排序,其空间开销远小于$O(n)$。
以一个具体例子来说明:假设我们有两个已排序的数组
[1, 2, 3, 6, 10]和[4, 5, 7, 9, 12, 14, 17],目标是将它们合并。在这个例子中,我们可以观察到: - 第二个数组中的最小元素
(4)需要插入到第一个数组的第四个位置以保持整体顺序, - 第一个数组中的最大元素(10)需要插入到第二个数组的第五个位置。因此,两个数组中的
[1, 2, 3]和[12, 14, 17]已经位于它们的最终位置,无需移动。我们实际上需要合并的部分是[6, 10]和[4, 5, 7, 9]。在这种情况下,我们只需要创建一个大小为 2 的临时数组,将
[6, 10]复制到其中,然后在原数组中将它们与[4, 5, 7, 9]合并。
Tim排序示例代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
def get_min_run(n):
"""
计算 minRun 长度,它是一个介于 32 到 64 之间的值。
"""
r = 0
while n >= 64:
r |= n & 1
n >>= 1
return n + r
def insertion_sort_for_timsort(arr, left, right):
"""
用于对小块 run 进行插入排序。
"""
for i in range(left + 1, right + 1):
key = arr[i]
j = i - 1
while j >= left and arr[j] > key:
arr[j + 1] = arr[j]
j -= 1
arr[j + 1] = key
def merge(arr, l, m, r):
"""
归并两个已排序的子数组。
arr[l...m] 和 arr[m+1...r]
"""
len1, len2 = m - l + 1, r - m
left_arr = arr[l: l + len1]
right_arr = arr[m + 1: m + 1 + len2]
i, j, k = 0, 0, l
while i < len1 and j < len2:
if left_arr[i] <= right_arr[j]:
arr[k] = left_arr[i]
i += 1
else:
arr[k] = right_arr[j]
j += 1
k += 1
while i < len1:
arr[k] = left_arr[i]
i += 1
k += 1
while j < len2:
arr[k] = right_arr[j]
j += 1
k += 1
def timsort(arr):
n = len(arr)
min_run = get_min_run(n)
# 第一阶段:对每个 run 进行插入排序
for i in range(0, n, min_run):
end = min(i + min_run - 1, n - 1)
insertion_sort_for_timsort(arr, i, end)
# 第二阶段:归并 runs
size = min_run
while size < n:
for left in range(0, n, 2 * size):
mid = min(left + size - 1, n - 1)
right = min((left + 2 * size - 1), n - 1)
if mid < right:
merge(arr, left, mid, right)
size *= 2
return arr
12. 内省排序
内省排序(Introsort)是由大卫·穆塞尔在1997年设计的排序算法。这个排序算法首先从快速排序开始,当递归深度超过一定深度(深度为排序元素数量的对数值)后转为堆排序。采用这个方法,内省排序既能在常规数据集上实现快速排序的高性能,又能在最坏情况下仍保持 $O(n\log n)$ 的时间复杂度。由于这两种算法都属于比较排序算法,所以内省排序也是一个比较排序算法。
为什么内省排序如此高效?
- 结三者优点:内省排序利用了快速排序的平均高效性,堆排序的最坏情况保证,以及插入排序在小数组上的高效率。
- 防性能退化:它的主要优势在于避免了快速排序最坏情况下的灾难性性能,使其在任何输入数据下都能稳定地保持 O(nlogn) 的时间复杂度。
- 实性:内省排序的这种自适应特性使其成为一种非常实用的排序算法,被 C++ 标准模板库(STL)中的 std::sort 所采用,是当今最常用的排序算法之一。
内省排序规则描述
- 首选快速排序:
- 算法开始时,像传统的快速排序一样,选取一个基准元素进行分区,并对子数组进行递归调用。快速排序在平均情况下表现最好,所以它是首选。
- 监控递归深度:
- 内省排序会跟踪快速排序的递归深度。它设置一个最大递归深度阈值,通常为 $2×log2(n)$ 其中 n 是原始数组的大小。
- 退化时切换:
- 如果递归深度超过这个阈值,这意味着快速排序的性能正在退化(例如,因为基准元素选择不佳,导致分区不平衡)。为了避免最坏情况的 $O(n^2)$ 性能,算法会立即切换到堆排序。
- 堆排序保证了最坏时间复杂度为 $O(nlogn)$,因此可以有效地防止性能崩溃。
- 处理小数组:
- 当递归到非常小的子数组时(例如,大小小于16),内省排序会停止递归,并切换到插入排序。这是因为插入排序在处理小规模数组时效率非常高,常数开销比快速排序小得多。
内省排序示例代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
import math
# 常量:小数组的阈值,低于此值则使用插入排序
SMALL_ARRAY_SIZE = 16
def insertion_sort_for_intro(arr, low, high):
"""
对小数组进行插入排序。
"""
for i in range(low + 1, high + 1):
key = arr[i]
j = i - 1
while j >= low and arr[j] > key:
arr[j + 1] = arr[j]
j -= 1
arr[j + 1] = key
def partition(arr, low, high):
"""
快速排序的分区函数。
"""
pivot = arr[high]
i = low - 1
for j in range(low, high):
if arr[j] <= pivot:
i += 1
arr[i], arr[j] = arr[j], arr[i]
arr[i + 1], arr[high] = arr[high], arr[i + 1]
return i + 1
def heapify(arr, n, i, start_index):
"""
堆排序的堆化函数,在指定的子数组范围内操作。
"""
largest = i
left = 2 * (i - start_index) + 1 + start_index
right = 2 * (i - start_index) + 2 + start_index
if left < n + start_index and arr[left] > arr[largest]:
largest = left
if right < n + start_index and arr[right] > arr[largest]:
largest = right
if largest != i:
arr[i], arr[largest] = arr[largest], arr[i]
heapify(arr, n, largest, start_index)
def heap_sort_for_intro(arr, low, high):
"""
堆排序,对指定的子数组进行排序。
"""
n = high - low + 1
start_index = low
for i in range(n // 2 - 1, -1, -1):
heapify(arr, n, start_index + i, start_index)
for i in range(n - 1, 0, -1):
arr[start_index + i], arr[start_index] = arr[start_index], arr[start_index + i]
heapify(arr, i, start_index, start_index)
def introsort_helper(arr, low, high, depth_limit):
"""
内省排序的递归辅助函数。
"""
n = high - low + 1
if n <= SMALL_ARRAY_SIZE:
insertion_sort_for_intro(arr, low, high)
return
if depth_limit == 0:
heap_sort_for_intro(arr, low, high)
return
# 使用三中值法选择更好的基准
mid = (low + high) // 2
arr[mid], arr[high] = arr[high], arr[mid]
pi = partition(arr, low, high)
# 递归调用,并递减递归深度限制
if pi > low:
introsort_helper(arr, low, pi - 1, depth_limit - 1)
if pi < high:
introsort_helper(arr, pi + 1, high, depth_limit - 1)
def introsort(arr):
"""
内省排序主函数。
"""
n = len(arr)
if n <= 1:
return arr
# 设置递归深度限制
depth_limit = 2 * math.floor(math.log2(n))
introsort_helper(arr, 0, n - 1, depth_limit)
return arr
基础排序算法变体
13. 鸡尾酒排序
鸡尾酒排序(Cocktail shaker sort),亦为定向冒泡排序,鸡尾酒搅拌排序,搅拌排序(也可以视作选择排序的一种变形),涟漪排序,来回排序或快乐小时排序,是冒泡排序的一种变形。此算法与冒泡排序的不同处在于排序时是以双向在序列中进行排序。
鸡尾酒排序等于是冒泡排序的轻微变形。不同的地方在于从低到高然后从高到低,而冒泡排序则仅从低到高去比较序列里的每个元素。他可以得到比冒泡排序稍微好一点的性能,原因是冒泡排序只从一个方向进行比对(由低到高),每次循环只移动一个项目。
以序列(2,3,4,5,1)为例,鸡尾酒排序只需要访问一次序列就可以完成排序,但如果使用冒泡排序则需要四次。但是在随机数序列的状态下,鸡尾酒排序与冒泡排序的效率与其他众多排序算法相比均比较低。
鸡尾酒排序规则描述
- 从左到右扫描:
- 从数组的起点开始,向右遍历。
- 在遍历过程中,像冒泡排序一样,比较并交换相邻的元素,确保较大的元素“冒泡”到右侧。
- 在这次扫描结束时,当前最大的元素会被移动到数组的最右端。
- 从右到左扫描:
- 从上一次扫描的终点(最右端)开始,向左遍历。
- 同样,比较并交换相邻的元素,确保较小的元素“冒泡”到左侧。
- 在这次扫描结束时,当前最小的元素会被移动到数组的最左端。
- 缩小范围:
- 每次双向扫描完成后,数组的最左端和最右端都已确定了一个排序好的元素。
- 因此,下一轮的扫描范围可以缩小,即将左边界向右移动一位,右边界向左移动一位。
- 重复:
- 重复步骤1至3,直到扫描范围内没有发生任何交换,这表明数组已经完全有序。
鸡尾酒排序演示
鸡尾酒排序示例代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
def cocktail_sort(arr):
n = len(arr)
swapped = True
start = 0
end = n - 1
while swapped:
swapped = False
# 从左到右冒泡
for i in range(start, end):
if arr[i] > arr[i + 1]:
arr[i], arr[i + 1] = arr[i + 1], arr[i]
swapped = True
# 如果没有发生交换,说明排序已完成
if not swapped:
break
swapped = False
end -= 1
# 从右到左冒泡
for i in range(end - 1, start - 1, -1):
if arr[i] > arr[i + 1]:
arr[i], arr[i + 1] = arr[i + 1], arr[i]
swapped = True
start += 1
return arr
14. 梳排序
梳排序(Comb Sort)是一种改进版的冒泡排序,旨在解决冒泡排序中效率低下的乌龟(turtle)问题。
乌龟问题: 在冒泡排序中,如果一个很小的元素位于数组的末尾,它需要经过很多次比较和交换,才能慢慢地“冒泡”到前面。这个过程非常缓慢,就像乌龟爬行一样,严重拖慢了整个排序的效率。
梳排序的核心思想是通过引入一个步长(gap)来克服这个问题。它不像冒泡排序那样只比较相邻的元素,而是比较相隔一个步长的两个元素。
通过使用步长,梳排序能迅速将那些距离正确位置很远的元素(即“乌龟”)移动到位。当步长逐渐减小并最终变为1时,它就能处理那些相邻的、需要精细调整的元素。这种先大刀阔斧、后精雕细琢的策略,使得梳排序在平均情况下的性能显著优于冒泡排序,但它的最坏时间复杂度仍然是 $O(n^2)$。
梳排序规则描述
- 初始化步长:设定一个大于1的初始步长。通常取数组长度除以一个被称为收缩因子(shrink factor)的常数,例如 1.3。
- 比较与交换:使用这个步长进行一轮遍历,比较相隔步长的元素。如果前一个元素大于后一个,则进行交换。
- 缩小步长:完成一轮遍历后,将步长除以收缩因子,然后取整数。
- 重复:重复步骤2和3,直到步长变为1。
- 最终阶段:当步长为1时,梳排序就退化成了冒泡排序。这时,再进行一轮或多轮冒泡排序,直到没有元素需要交换,整个数组就排序完成了。
梳排序演示
梳排序示例代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
def comb_sort(arr):
n = len(arr)
gap = n
shrink_factor = 1.3
swapped = True
while gap > 1 or swapped:
# 更新步长
gap = int(gap / shrink_factor)
if gap < 1:
gap = 1
swapped = False
# 遍历整个数组,进行比较和交换
for i in range(n - gap):
if arr[i] > arr[i + gap]:
arr[i], arr[i + gap] = arr[i + gap], arr[i]
swapped = True
return arr
15. 希尔排序
1959年Shell发明,第一个突破O(n2)的排序算法,希尔排序可以看作是一个冒泡排序或者插入排序的变形。
希尔排序是基于插入排序的以下两点性质而提出改进方法的:
- 插入排序在对几乎已经排好序的数据操作时,效率高,即可以达到线性排序的效率
- 但插入排序一般来说是低效的,因为插入排序每次只能将数据移动一位
它与插入排序的不同之处在于,它会优先比较距离较远的元素。希尔排序在每次的排序的时候都把数组拆分成若干个序列,一个序列的相邻的元素索引相隔的固定的距离gap,每一轮对这些序列进行冒泡或者插入排序,然后再缩小gap得到新的序列一一排序,直到gap为1
希尔排序规则描述 1959年Shell发明,第一个突破O(n2)的排序算法,是简单插入排序的改进版。它与插入排序的不同之处在于,它会优先比较距离较远的元素。希尔排序又叫缩小增量排序。
- 选择一个增量序列t1,t2,…,tk,其中ti>tj,tk=1;
- 按增量序列个数k,对序列进行k 趟排序;
- 每趟排序,根据对应的增量ti,将待排序列分割成若干长度为m 的子序列,分别对各子表进行直接插入排序。仅增量因子为1 时,整个序列作为一个表来处理,表长度即为整个序列的长度。
希尔排序演示
希尔排序示例代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
def shell_sort(list):
n = len(list)
# 初始步长
gap = n // 2
while gap > 0:
for i in range(gap, n):
# 每个步长进行插入排序
temp = list[i]
j = i
# 插入排序
while j >= 0 and j-gap >= 0 and list[j - gap] > temp:
list[j] = list[j - gap]
j -= gap
list[j] = temp
# 得到新的步长
gap = gap // 2
return list
16. 原地归并排序
原地归并排序(In-place Merge Sort)是归并排序的一种变体,它的主要目标是将空间复杂度从 O(n) 降到 O(1)。原地归并排序的挑战就在于如何在不使用额外数组的情况下完成合并操作。它通过一系列复杂的原地操作(例如旋转、反转等)来实现合并,避免了创建临时数组。
原地归并排序规则描述
同样是递归地将数组分成两半。但在合并阶段,它会:
- 找到两个已排序子数组中的逆序对。
- 利用一些精巧的算法(如 Juggling Algorithm 或 In-place merge algorithms based on block swaps)在不借助额外空间的情况下,将这些元素移动到正确的位置。
原地归并排序演示(流程和归并排序一致, 仅在交换元素的实现不同)
原地归并排序示例代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
def in_place_merge_sort(arr, left=0, right=None):
if right is None:
right = len(arr) - 1
if left < right:
mid = (left + right) // 2
in_place_merge_sort(arr, left, mid)
in_place_merge_sort(arr, mid + 1, right)
in_place_merge(arr, left, mid, right)
return arr
def in_place_merge(arr, left, mid, right):
"""
原地归并函数,将 arr[left..mid] 和 arr[mid+1..right] 合并。
"""
i = left
j = mid + 1
while i <= mid and j <= right:
if arr[i] <= arr[j]:
i += 1
else:
# 找到需要移动的元素
value = arr[j]
index = j
# 将比 arr[j] 大的元素向右移动
while index > i:
arr[index] = arr[index - 1]
index -= 1
# 将 arr[j] 插入到正确位置
arr[i] = value
# 更新指针和 mid 值
i += 1
mid += 1
j += 1
17. 鸽巢排序
鸽巢排序(Pigeonhole Sort)是一种非比较排序算法,它适用于待排序元素的数量 n 和元素值的范围 N 大致相等的情况。它的核心思想基于鸽巢原理(也称抽屉原理)。
鸽巢排序就像是将一群鸽子放入鸽笼。如果每个笼子最多只能放一只鸽子,那么鸽子总数就不能超过笼子总数。换句话说,如果鸽子数量等于笼子数量,每个笼子恰好放一只鸽子,就可以保证鸽子之间不会相互挤占。
鸽巢排序与计数排序(Counting Sort)非常相似。它们都通过使用一个辅助数组来避免比较。主要区别在于:
- 计数排序的辅助数组存储的是元素的出现次数。
- 鸽巢排序的辅助数组存储的是实际的元素(或者是一个列表,当存在重复元素时)。 因为这个区别,鸽巢排序在处理包含重复元素的数组时,需要一个稍微复杂的结构(比如列表)来存储,而计数排序只需要简单地增加计数器的值。
鸽巢排序规则描述
- 确定范围:首先,找到待排序数组中的最小值和最大值,从而确定元素的取值范围。
- 创建“鸽巢”:创建一个与元素取值范围大小相等的辅助数组,这个数组的每个索引都代表一个唯一的元素值。你可以把这个辅助数组看作是“鸽巢”的集合。
- 放入“鸽子”:遍历原始数组,将每个元素“放入”其对应的“鸽巢”。如果一个“鸽巢”中已经有元素,就将新的元素添加到该位置的列表中。这确保了算法的稳定性。
- 收集结果:遍历“鸽巢”数组,按照索引的顺序,将每个“鸽巢”中的元素依次取出,重新放回原始数组。
鸽巢排序示例代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
def pigeonhole_sort(arr):
if not arr:
return []
# 找到最大值和最小值
min_val = min(arr)
max_val = max(arr)
# 确定鸽巢的数量
size = max_val - min_val + 1
# 创建鸽巢,每个鸽巢都是一个列表,用于存储元素
holes = [[] for _ in range(size)]
# 将元素放入对应的鸽巢中
for x in arr:
holes[x - min_val].append(x)
# 从鸽巢中按顺序取出元素
result_index = 0
for hole in holes:
for x in hole:
arr[result_index] = x
result_index += 1
return arr
不常见的排序算法
18. 奇偶排序
奇偶排序(Odd–even sort),或奇偶换位排序、砖排序,是一种相对简单的排序算法,最初发明用于有本地互连的并行计算。这是与冒泡排序特点类似的一种比较排序。
该算法中,通过比较数组中相邻的(奇-偶)位置数字对,如果该奇偶对是错误的顺序(第一个大于第二个),则交换。下一步重复该操作,但针对所有的(偶-奇)位置数字对。如此交替进行下去。
奇偶排序最初是为了在并行处理器上使用而设计的。在并行计算环境中,因为奇数阶段的比较和偶数阶段的比较是独立的,它们可以同时进行。
奇偶排序规则描述
奇偶排序的工作流程是交替进行两个阶段的比较和交换操作
- 奇数阶段(Odd Phase):比较和交换所有奇数索引上的元素和它们右边的相邻元素。
- 比如,比较
arr[1]和arr[2],arr[3]和arr[4],arr[5]和arr[6],以此类推。
- 比如,比较
- 偶数阶段(Even Phase):比较和交换所有偶数索引上的元素和它们右边的相邻元素。
- 比如,比较
arr[0]和arr[1],arr[2]和arr[3],arr[4]和arr[5],以此类推。
- 比如,比较
算法会交替重复这两个阶段,直到在整个一轮的奇数阶段和偶数阶段中都没有发生任何交换,这表明数组已经完全排序。
奇偶排序演示
奇偶排序示例代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
def odd_even_sort(arr):
n = len(arr)
is_sorted = False
while not is_sorted:
is_sorted = True
# 奇数阶段
for i in range(1, n - 1, 2):
if arr[i] > arr[i + 1]:
arr[i], arr[i + 1] = arr[i + 1], arr[i]
is_sorted = False
# 偶数阶段
for i in range(0, n - 1, 2):
if arr[i] > arr[i + 1]:
arr[i], arr[i + 1] = arr[i + 1], arr[i]
is_sorted = False
return arr
19. 侏儒排序
侏儒排序(Gnome Sort)或愚人排序(Stupid Sort)是一种排序算法,最初在2000年由伊朗计算机工程师哈米德·萨尔巴齐-阿扎德(Hamid Sarbazi-Azad)提出,他称之为“愚人排序”。此后迪克·格鲁纳也描述了这一算法,称其为“侏儒排序”。此算法类似于插入排序,但是移动元素到它该去的位置是通过一系列类似冒泡排序的移动实现的。从概念上讲侏儒排序非常简单,甚至不需要嵌套循环。它的平均运行时间是 $O(n^2)$, 如果列表已经排序好则只需 $O(n)$ 的运行时间。
它的基本思想是遍历数组,一旦发现逆序就进行交换,并向后退一步重新检查
侏儒排序可以想象成一个花园里的侏儒,他正在整理一排花盆。他从左到右检查,如果发现当前花盆比它旁边的花盆高,他就会把它们交换过来,然后退后一步,重新检查这两盆花,以确保它们的新位置是正确的。他会一直重复这个过程,直到遍历完整个花园,并且所有花盆都按顺序排列好。
侏儒排序规则描述
- 从头开始:设定一个游标,初始指向数组的第一个元素(索引
i = 0)。 - 前进与比较:
- 如果游标i在数组开头(
i = 0),则简单地向前移动一位(i++)。 - 如果当前元素
arr[i]大于或等于前一个元素arr[i-1],说明顺序正确,继续向前移动(i++)。
- 如果游标i在数组开头(
- 逆序与交换:
- 如果当前元素
arr[i]小于前一个元素arr[i-1],说明发生了逆序。 - 这时,交换这两个元素的位置,然后将游标向后退一步(
i--),回到上一个位置重新检查。
- 如果当前元素
- 重复:重复上述步骤,直到游标移动到数组的末尾,整个数组就排好序了。
侏儒排序演示
侏儒排序示例代码
1
2
3
4
5
6
7
8
9
def gnome_sort(arr):
i = 0
while i < len(arr):
if i == 0 or arr[i] >= arr[i - 1]:
i += 1
else:
arr[i], arr[i - 1] = arr[i - 1], arr[i]
i -= 1
return arr
20. 平滑排序
平滑排序算法是堆排序的变体,由 Edsger Wybe Dijkstra 于1981年提出。它是一种不稳定的比较排序算法,主要用于对大量数据进行排序。它是堆排序的变种,具有较高的效率,并且其最优时间复杂度为 $O(N)$,在平均、最坏情况下,它的时间复杂度也保持在 $O(NlogN)$,但常数因子比堆排序更大。
平滑排序算法基于一个概念叫做“平滑堆”。它使用一个特定的堆结构,该结构使得不需要让元素下沉时几乎一定会到堆的最后面。
平滑排序会建多个按后序遍历记录的堆,每个堆的大小、遍历方法都是确定的。其中,最后一个堆的堆顶最大,倒数第二个堆的堆顶第二大,以此类推。
要弄明白这个结构,首先看齐这个数列(莱恩昂多数列):
\[f(x) = \begin{cases} 1 & x \le 2 \\ f(x-1) + f(x-2) + 1 & x > 2 \end{cases}\]比如,前几项莱恩昂多数列是:1,1,3,5,9,15,25,41,67,……
这个数列与建堆有很大的联系。如果一个平滑堆有 $f(x)$ 个数,那么这个平滑堆的左子树就有 $f(x−1)$ 个数,这个平滑堆的右子树就有 $f(x−2)$ 个数,这样的话,这个平滑堆的元素量就刚好是 $f(x−1)(左子树的元素个数)+f(x−2)(右子树的元素个数)+1(根节点)=f(x)$,这样有重大的作用。
假如我们已经算出了莱恩昂多数列的前 i 项,那么一个大小为 $f(i)$ ,开头为 j 的平滑堆不需要额外的空间,就可以实现 $O(1)$ 找儿子。找右儿子可直接访问 $a(j+f(i)−2)$,找左儿子可直接访问 $a(j+f(i−1)−1)$。
那么,如果给 N 个数排序,而不是 $f(i)$ 个数,该怎么办呢?其实对于任意一个正整数 N,一定可以用若干个莱恩昂多数的和表示,因为莱恩昂多数中包含两个1,而且每一项都是奇数。所以,平滑排序建的堆是可以计算的。这就是为什么平滑排序不使用完美二叉树,为了保证一定能建出平滑堆。
建好多个堆之后,最大的数已经在最右边,那么把最大的数当成一个独立的数,不再是最后一个堆的堆顶,此时那个堆就被切分成两个堆,现在场上的堆就多一个。
然后移动堆顶的元素,使它们重新有序。(注意,只将堆顶的元素排序,而就只有最后两个数无序,所以用插入排序,在插入时先比较这个堆的两个孩子,选出较大的,再与下一个堆的堆顶比较,若更小则继续传送元素,否则留下它,并不断将它与较大的孩子交换)排序后,次大的数和次次大的数又已经在最右边。
重复这两个操作,直到所有的数归位。
这种堆结构保证了排序操作的高效性。
平滑排序在理论上非常优雅,它试图结合插入排序在有序数据上的高效性和堆排序在最坏情况下的可靠性。然而,由于其实现的高度复杂性,它并没有像快速排序或归并排序那样被广泛应用。
平滑排序规则描述
- 构建莱昂纳多堆序列:
- 算法从左到右遍历输入数组,将每个元素一个接一个地插入到由莱昂纳多堆组成的序列中。
- 这个过程是动态的,算法会根据新元素的值,合并或拆分现有的莱昂纳多堆,确保堆的根节点始终按升序排列。
- 排序:
- 堆序列构建完成后,最大的元素位于最后一个堆的根部。
- 算法从右向左遍历,每次都将最大的元素(即当前堆序列的根)取出,放到数组的末尾,然后重新调整剩余的堆结构。
- 这个过程类似于堆排序中的逐一取出最大值。
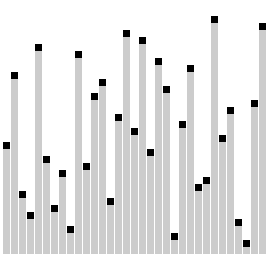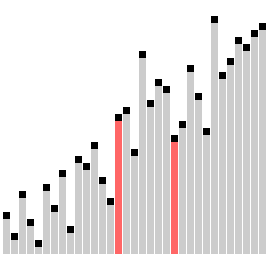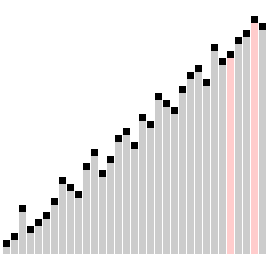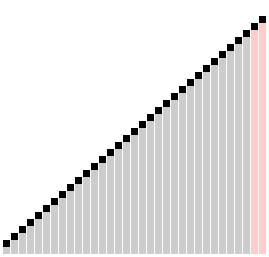
平滑排序演示
对一个基本有序的数组进行平滑排序。顶部的横条显示了树形结构。
平滑排序示例代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
# 莱昂纳多数列的预计算
LEONARDO = [1, 1, 3, 5, 9, 15, 25, 41, 67, 109, 177, 287, 465, 753]
def get_leo(n):
if n >= len(LEONARDO):
# 动态扩展莱昂纳多数列
while n >= len(LEONARDO):
LEONARDO.append(LEONARDO[-1] + LEONARDO[-2] + 1)
return LEONARDO[n]
def smooth_sort(arr):
n = len(arr)
if n <= 1:
return arr
p = 1
q = 1
# 第一阶段:构建莱昂纳多堆序列
for i in range(n):
if (p & 3) == 3:
p >>= 2
q += 1
elif get_leo(q - 1) == i + 1:
p <<= 1
q -= 1
else:
p <<= 1
q += 1
# 向上调整堆
s = p
while (s & 1) == 0:
s >>= 1
while s > 1:
r = s >> 1
if arr[i] > arr[i - get_leo(r) - get_leo(r-1)]:
break
arr[i], arr[i - get_leo(r) - get_leo(r-1)] = arr[i - get_leo(r) - get_leo(r-1)], arr[i]
i = i - get_leo(r) - get_leo(r-1)
s = r
# 第二阶段:逐个取出最大元素
for i in range(n - 1, -1, -1):
if q == 1:
arr[i], arr[0] = arr[0], arr[i]
p >>= 1
q += 1
else:
if get_leo(q - 1) == i + 1:
p >>= 1
q -= 1
else:
p >>= 1
q -= 1
# 向下调整堆
s = p
while (s & 1) == 0:
s >>= 1
while s > 1:
r = s >> 1
# 确定最大的子节点
largest_child_idx = i - get_leo(r) - get_leo(r-1)
if arr[largest_child_idx] < arr[i - get_leo(r) + 1]:
largest_child_idx = i - get_leo(r) + 1
if arr[i] >= arr[largest_child_idx]:
break
arr[i], arr[largest_child_idx] = arr[largest_child_idx], arr[i]
i = largest_child_idx
s = r
return arr
21. 耐心排序
耐心排序(Patience Sort)是一种非常独特的排序算法,它利用了游戏“耐心(Patience)”的核心思想,来对数据进行排序。它最常被用来寻找最长递增子序列(Longest Increasing Subsequence, LIS)。
耐心排序的基本思想可以概括为:将牌堆中的牌逐一分到不同的牌堆中,并遵循特定规则,最终再将这些牌堆合并。
耐心排序规则描述
- 构建牌堆(Building Piles)
- 算法从头到尾遍历待排序的序列。
- 每拿到一个元素(一张牌),就将其放到当前所有牌堆中最左边的一个牌堆的顶上,但前提是这个元素小于或等于该牌堆顶部的元素。
- 如果这个元素比所有牌堆顶部的元素都大,那么就新创建一个牌堆,将这个元素作为新的牌堆的第一个元素。
- 这个过程会产生一系列牌堆,它们的顶部元素从左到右是严格递增的。
- 合并牌堆(Merging Piles)
- 牌堆创建完成后,算法会使用一个类似于多路归并的方法,将所有牌堆合并起来。
- 每次从所有牌堆的顶部,找到并取出最小的那个元素,将其放入最终的排序结果中。
- 这个过程会持续进行,直到所有牌堆都为空。
耐心排序示例代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
import bisect
import heapq
def patience_sort(arr):
"""
使用耐心排序对列表进行排序。
"""
if not arr:
return []
# 第一步:构建牌堆
piles = []
for x in arr:
# 使用 bisect_left 找到第一个大于或等于 x 的牌堆
i = bisect.bisect_left([pile[-1] for pile in piles], x)
if i < len(piles):
# 将 x 放入现有牌堆的顶部
piles[i].append(x)
else:
# 创建一个新牌堆
piles.append([x])
# 第二步:使用堆合并牌堆
# 将每个牌堆的顶部元素放入一个最小堆中
min_heap = [(pile[-1], i) for i, pile in enumerate(piles)]
heapq.heapify(min_heap)
# 结果列表
result = []
while min_heap:
# 取出最小元素及其所在的牌堆索引
val, pile_idx = heapq.heappop(min_heap)
result.append(val)
# 将该牌堆的下一个元素放入最小堆
piles[pile_idx].pop()
if piles[pile_idx]:
new_val = piles[pile_idx][-1]
heapq.heappush(min_heap, (new_val, pile_idx))
return result
不实用的排序算法
22. 图书馆排序
图书馆排序(英语:Library sort),或空位插入排序是一种排序算法 ,它基于插入排序,但在每两个元素之间存在空位,以便于加速随后的插入。
图书馆排序是一个比较理论化的算法,它的核心思想是利用稀疏数组(即在元素之间留有空隙的数组)来提高插入效率, 空间复杂度极高
这个名字来自一个比喻:
假设一名图书管理员在一个长架上按字母顺序来整理书,从左边A开头的书,一直到右边Z开头的书,书本之间没有空格。如果图书管理员有一本开头为B的新书,当他找到了这本书在B区中的正确位置,他将不得不把从该位置后一直到Z的每一本书向右移动,就只是为了腾出空位放置这本新书。这就是插入排序的原理。但是,如果他在每一字母区后留有额外的空间,只要在B区之后还有空间,他插入书时就只需要移动少数几本书,而不会移动后面所有的书,这是图书馆排序的原理。
图书馆排序规则描述 现在我们有大小为n个元素的数组。我们选择每两个元素之间的空位,那么我们将有一个最大的数组 $(1 +ε)n$。该算法在log n轮中工作。我们通过二分查找来找到插入的位置,然后交换后面的元素,直到我们命中一个空格。一旦结束,我们通过在每个元素之间插入空格来重新平衡最终的数组。
算法根据以下三个重要的步骤:
- 二分查找:我们在已经插入的元素中,二分查找这个元素应该插入的位置。这可以通过线性移动到阵列的左侧或右侧,如果您点击中间元素中的空格。
- 插入: 将元素插入到正确的位置,并且通过交换把后面的元素向右移动,直到空格。
- 重新平衡:在数组中的每对元素之间插入空格。这需要线性时间,并且由于算法只运行log n轮,总重新平衡只需要 $O(n log n)$ 时间。
图书馆排序示例代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
def insertion_sort_for_library(arr):
"""
一个简单的插入排序,用于对图书馆排序中的子数组进行排序。
"""
for i in range(1, len(arr)):
key = arr[i]
j = i - 1
while j >= 0 and key < arr[j]:
arr[j + 1] = arr[j]
j -= 1
arr[j + 1] = key
return arr
def library_sort(arr):
if not arr:
return []
n = len(arr)
# 创建一个稀疏数组,大小是原数组的两倍,用于在元素间留出空隙
# 使用 None 来表示空位
sparse_arr = [None] * (n * 2)
# 将第一个元素放入稀疏数组
sparse_arr[0] = arr[0]
count = 1
for i in range(1, n):
element_to_insert = arr[i]
# 寻找插入位置
# 由于稀疏数组中有空隙,这里需要处理 None
j = 0
while j < count and sparse_arr[j] is not None and element_to_insert > sparse_arr[j]:
j += 1
# 检查是否有足够的空隙
if sparse_arr[j] is not None and j < count:
# 没有足够的空隙,需要“重新平衡”数组
# 这里简单地使用插入排序来重新组织非None元素
temp = [x for x in sparse_arr if x is not None]
temp.append(element_to_insert)
temp = insertion_sort_for_library(temp)
# 将重新排序的元素放回稀疏数组
sparse_arr = [None] * (len(temp) * 2)
for k, item in enumerate(temp):
sparse_arr[k*2] = item
count = len(temp) * 2
else:
# 直接插入到空位
sparse_arr[j] = element_to_insert
count += 1
# 提取并返回排序好的元素
return [x for x in sparse_arr if x is not None]
23. Bogo排序
Bogo排序(英语:Bogosort)是个非常低效率的排序算法,通常用在教学或测试。其原理等同将一堆卡片抛起,落在桌上后检查卡片是否已整齐排列好,若非就再抛一次。其名字源自”bogus”,又称bozo sort、blort sort或无限猴子排序
其平均时间复杂度是 O(n × n!),在最坏情况所需时间是无限
规则描述
- 检查:检查待排序的列表是否已经有序。
- 打乱:如果列表未排序,就将列表中的元素随机地打乱(重新排列)。
- 重复:重复步骤1和2,直到列表碰巧被排好序为止。
示例代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
import random
def bogo_sort(arr):
"""
一个 Bogo 排序的 Python 实现。
"""
def is_sorted(arr):
# 检查列表是否已排序
for i in range(len(arr) - 1):
if arr[i] > arr[i + 1]:
return False
return True
while not is_sorted(arr):
random.shuffle(arr) # 随机打乱列表
return arr
24. 珠排序
珠排序(Bead Sort),又称重力排序(Gravity Sort),是一种独特的、非比较排序算法。它的基本思想是模拟珠子在杆子上受重力作用下下落的过程,从而达到排序的目的。
尽管珠排序在理论上非常有趣,并且在某些情况下可以达到线性时间复杂度,但它有几个严重的缺点:
- 硬件依赖:它需要特殊的并行硬件来真正实现其 O(1) 的潜力。
- 空间开销:如果数字很大,所需的内存空间会呈指数级增长。
- 仅限正整数:它只能对正整数进行排序。
规则描述
珠排序通常通过一个二维数组来表示,其中行代表数字,列代表珠子。它的操作流程可以这样形象化:
- 准备:
- 想象你有一系列垂直的杆子(代表数值),每根杆子上都穿有珠子。
- 珠子的数量由待排序数组中的元素值决定。例如,如果数组中有数字 5,那就准备 5 个珠子。
- “穿珠子”:
- 将待排序数组中的每个元素转化为一排珠子。
- 比如,要排序的数组是 [5, 2, 4]。
- 在第一排,从左到右穿上 5 个珠子。
- 在第二排,从左到右穿上 2 个珠子。
- 在第三排,从左到右穿上 4 个珠子。
- “施加重力”:
- 想象这些珠子都挂在杆子上,现在我们施加重力。
- 所有的珠子都会向下“下落”,直到被下面的珠子或地面挡住。
- 由于上面的珠子数量总是不小于下面的珠子,它们最终会形成一个阶梯状的排列。
- 读取结果:
- 珠子稳定后,每一行代表一个排序后的元素。
- 我们只需计算每一行所包含的珠子数量,就可以得到排序后的结果。
示例代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
def bead_sort(arr):
"""
珠排序(Bead Sort)的 Python 实现。
该算法仅适用于非负整数。
"""
if not arr or any(x < 0 for x in arr):
# 珠排序只适用于非负整数
return "错误:珠排序仅支持非负整数。"
if len(arr) <= 1:
return arr
# 找到最大值,它决定了珠子板的宽度
max_val = max(arr)
# 创建一个二维列表来模拟珠子板
# 宽度为 max_val,高度为列表长度
board = [[0] * max_val for _ in range(len(arr))]
# “穿珠子”:将数字转化为珠子
for i, num in enumerate(arr):
for j in range(num):
board[i][j] = 1
# “施加重力”:模拟珠子下落
# 从上到下,从右到左遍历珠子板
for j in range(max_val):
beads_in_col = 0
# 统计每一列的珠子数量
for i in range(len(arr)):
if board[i][j] == 1:
beads_in_col += 1
# 将珠子移到底部
for i in range(len(arr) - 1, -1, -1):
if beads_in_col > 0:
board[i][j] = 1
beads_in_col -= 1
else:
board[i][j] = 0
# “读取结果”:将珠子板转化为排序后的列表
result = []
for i in range(len(arr)):
bead_count = sum(board[i])
result.append(bead_count)
return result
25. 煎饼排序
煎饼排序(Pancake Sort)是一种有趣的排序算法,它的灵感来源于一个现实中的问题:如何用锅铲最少次地将一叠大小不一的煎饼按从大到小的顺序叠放?
煎饼排序不实用的主要原因在于它的时间复杂度。
对比其他排序算法
- 快速排序、归并排序、堆排序:这些算法的平均时间复杂度都是 $O(nlogn)$。对于一个有 10000 个元素的列表,它们可能只需要几十万次操作就能完成排序,而煎饼排序则需要高达一亿次操作。
- 冒泡排序、插入排序:这些算法的时间复杂度也是 $O(n^2)$,但它们通常在小数组上表现更好,或者实现起来更简单。煎饼排序虽然也属于这一类,但其“翻转”操作的实现相对复杂,并没有带来任何性能上的优势。
规则描述
煎饼排序的核心操作是翻转(flip)。你不能拿起一个煎饼然后直接把它放到中间,你只能用一个锅铲插入某一位置,然后将该位置以上的所有煎饼一起翻转。
这个算法的目标就是通过这种“翻转”操作,将数组(煎饼)从大到小(或从小到大)排列。它的基本流程可以概括为:
- 找到最大元素:从当前未排序的数组中,找到最大的元素。
- 将其移到顶部:
- 如果最大元素不在顶部(索引为0),就用一次“翻转”操作,将它翻到数组的最顶部。
- 将其移到底部:
- 现在最大的元素已经在顶部了,再用一次“翻转”操作,将它连同整个数组一起翻转。
- 这样,当前最大的元素就被放到了数组的最后,也就是它最终的排序位置。
- 重复:
- 将数组的有效长度减1,并对剩下的子数组重复上述步骤。
- 这个过程会持续进行,直到数组完全排序。
示例代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
def flip(arr, i):
"""
翻转数组 arr 中从 0 到 i 的部分
"""
start = 0
while start < i:
arr[start], arr[i] = arr[i], arr[start]
start += 1
i -= 1
def find_max_index(arr, n):
"""
找到数组中最大元素的索引
"""
max_idx = 0
for i in range(n):
if arr[i] > arr[max_idx]:
max_idx = i
return max_idx
def pancake_sort(arr):
"""
煎饼排序的 Python 实现
"""
n = len(arr)
# 从大到小排列,每次确定一个最大值
for current_size in range(n, 1, -1):
# 找到当前未排序部分中最大元素的索引
max_idx = find_max_index(arr, current_size)
# 如果最大元素不在当前末尾
if max_idx != current_size - 1:
# 第一步:将最大元素翻转到顶部
flip(arr, max_idx)
# 第二步:将顶部(最大)元素翻转到正确位置
flip(arr, current_size - 1)
return arr
26. 臭皮匠排序
臭皮匠排序(Stooge Sort) 的核心思想是:如果一个列表没有排序,那就把它分成三部分:前三分之二、后三分之二和中间。然后分别对这三部分进行递归排序,以确保前两个元素和后两个元素的相对位置是正确的。
臭皮匠排序不实用的核心原因在于其极低的效率, 其平均和最坏时间复杂度都达到了 $ O(n^{2.71}) $ 。这是一个非常糟糕的性能指标。
规则描述
- 边界:如果待排序的列表只有一个元素,那么它已经有序,直接返回。如果第一个元素比最后一个元素大,就交换它们。
- 排序:如果列表的长度大于2,就将列表分为三部分,每部分的长度约为 2n/3。
- 排序前三分之二的元素。
- 排序后三分之二的元素。
- 递归排序前三分之二的元素,以确保所有元素都处于正确的位置。
演示
示例代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
def stooge_sort(arr, low=0, high=None):
"""
一个递归的臭皮匠排序(Stooge Sort)的 Python 实现。
"""
if high is None:
high = len(arr) - 1
if low >= high:
return
# 如果第一个元素大于最后一个,交换它们
if arr[low] > arr[high]:
arr[low], arr[high] = arr[high], arr[low]
# 如果列表中有超过两个元素,进行递归
if (high - low + 1) > 2:
t = (high - low + 1) // 3
# 递归排序前三分之二
stooge_sort(arr, low, high - t)
# 递归排序后三分之二
stooge_sort(arr, low + t, high)
# 再次递归排序前三分之二,以确保正确排序
stooge_sort(arr, low, high - t)
return arr