海量积分数据实时排名处理方式
需求概述
积分排名在很多项目都会出现,大家都不会陌生,需求也很简单,积分排名主要满足以下需求:
- 查询用户名次。
- 查询TopN(即查询前N名的用户)
- 实时排名(很多项目是可选的)
当排序的数据量不大的时候,这个需求很容易满足,但是如果数据量很大的时候比如百万级、千万级甚至上亿的时候,或者有实时排名需求;这个时候要满足性能、低成本等需求,在设计上就变得复杂起来了
常规积分排名处理
这里列举下日常对于排名的常规做法和缺陷。
数据库解决方案
这是最简单的做法,数据存储在数据库里面,然后利用数据库做排序处理。
这里分两种情况:
单库/单表
参与排名的数据量小的时候的做法,所有数据存储在一张表上。
查询操作示例:
查询用户名次:
1
SELECT count(*) as rank FROM 积分表 WHERE 积分 > (SELECT 积分 FROM 积分表 WHERE uid=’用户ID’)
查询前N名:
1
SELECT uid, 积分 FROM 积分表 ORDER BY 积分 DESC LIMIT 0,N
分库/分表
对于这种情况数据不在一块,在查询操作上跟上面单表情况的区别就是,分库/分表需要做,查询任务切割和查询结果合并处理。
查询排名效率低,会造成扫描大量的记录,甚至全表扫描,性能低,在数据量大、高并发的情况下这种方案是不可用的。
采用常规排序算法
思路上就是把积分排序处理从数据库转移出来,自己实现排序和查询处理。
实际排名业务的特点:
- 每次用户的积分更新都会在一个小的积分范围内波动。
- 已有的积分数据都是已排序的。
常见的几种排序算法大家都熟知这里就不列举了。
缺陷:
对于海量数据排序处理,简单的使用常规排序算法并不合适,要么就是排序造成大量的数据移动、要么就是对已排序的数据查询名次效率不高。
高效的排名算法
前面的排名算法都是针对积分进行排序,然后通过统计积分高于自己的人数获得排名。
要想知道某个用户的名次,只需要知道比这个用户高分的人数,不一定需要对积分做排序。
在这里换个思路不对积分进行排序,仅仅是统计每个积分区间的人数,用积分区间的形式去统计相应的人数,下面是算法描述。
根据积分范围创建平衡二叉树
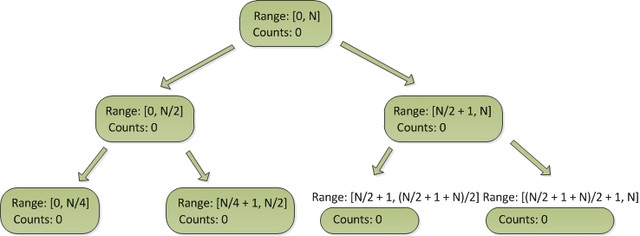
设[0, N]为积分范围, 构造的平衡二叉树如下图。
每个节点包含两个数据字段(除了指针):
- Range: 表示积分范围。
- Counts: 表示当前积分区间包含多少人。
积分的区间的划分是根据平分的方式,把当前积分范围一分为二生成两个子节点,然后递归的重复该步骤,直到积分区间无法划分为止(即区间[x, y], x == y)
例子:
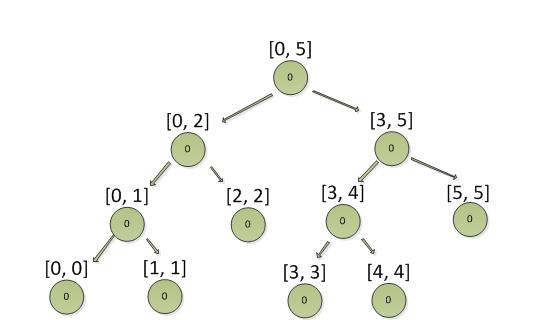
假设积分范围为: [0, 5], 构造的平衡二叉树如下图:
节点内的数据表示当前积分区间的人数。
从上图可以看出来,所有积分都在叶子节点,叶子节点即最小粒度的积分区间。
统计相应积分区间的人数
这里主要有两种操作:
假设积分为i
添加积分
添加积分的过程就是查找积分i, 同时累加查找过程经过的节点计数。
下面给出操作例子,注意观察操作路径。
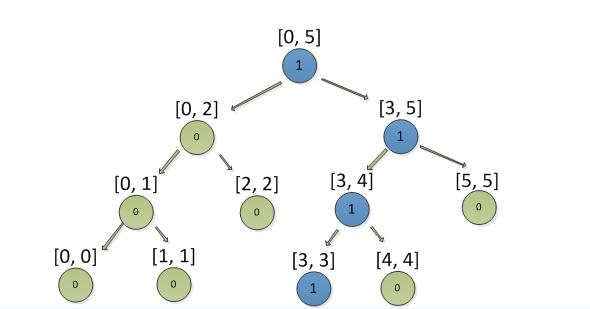
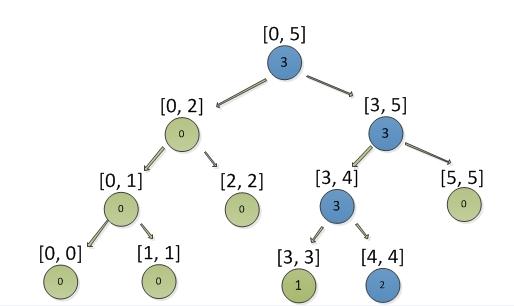
例: 需要添加积分3, 结果如下图
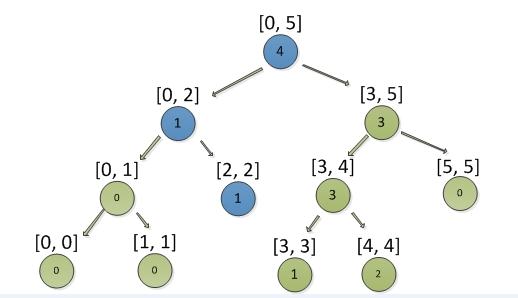
接着在添加积分4,结果如下图
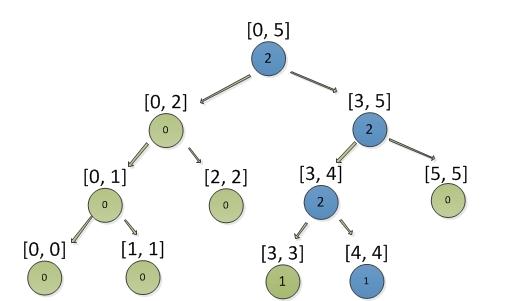
接着再添加积分4,结果如下图
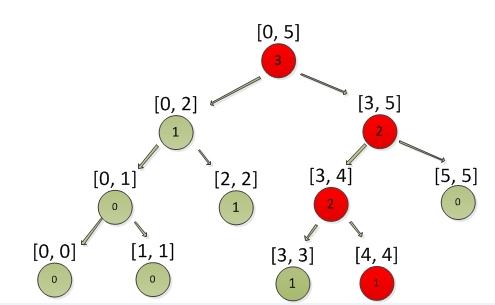
接着添加积分2,结果如下图
删除积分
删除积分的过程也是查找积分i, 区别是查找过程经过的节点计数全部减1。
只有积分是存在的情况下,才能做删除操作,另外用一组标记,标识积分是否存在,这里就不列举了。
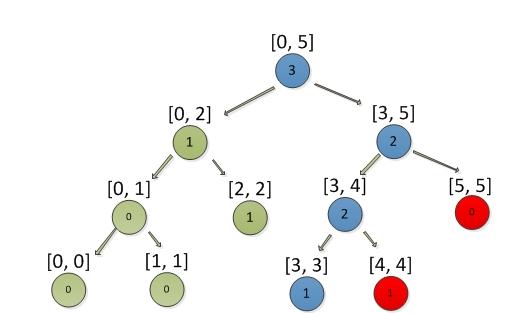
例子: 删除积分4, 结果如下图
查询名次操作
查询某个积分的排名的过程也是查找积分i的过程,下面是查找过程统计节点计数的算法:
对于查找路径上的任意节点,如果积分在左节点区间,则累加右节点区间的计数。
最终累加计数的结果加1即是积分的名次
例子: 查找积分3的名次
蓝色节点是查找积分3经过的路径,红色节点是需要累加的计数值。
最终结果是:0 + 1 + 1, 积分3的名次是第2名
从上面的算法可以看出,对平衡二叉树的操作,算法复杂度是O(log N), N是最大积分。
在积分范围不变的情况下,算法复杂度是稳定的,跟用户量无关,因此可以实现海量用户积分排名、实时排名算法需要。
对于海量积分数据实时排名、这里给出的是核心算法,实际业务的时候还需要增加一些额外的处理,比如uid于积分的映射表用于记录用户历史积分、积分与uid的映射表用于TopN这种查询前N名的需求、数据持久化、高可用等需求。